50% Maths and 50 % Physics!!
 Let
a
x
5
−
b
x
4
+
c
x
3
−
d
x
2
+
e
x
−
f
=
0
be an equation which has 5 real roots
α
1
,
α
2
,
α
3
,
α
4
and
α
5
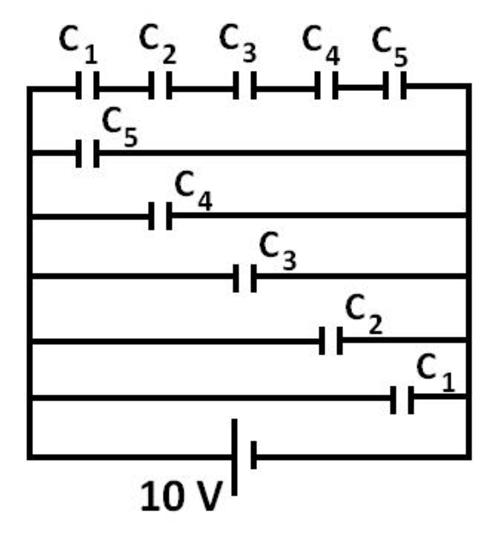
, which are the values of capacitance of the 5 capacitors shown in the figure (not necessarily in order). Find the capacitance of a single capacitor which can replace the combination and store the same charge (as the combination).
Let
a
x
5
−
b
x
4
+
c
x
3
−
d
x
2
+
e
x
−
f
=
0
be an equation which has 5 real roots
α
1
,
α
2
,
α
3
,
α
4
and
α
5
, which are the values of capacitance of the 5 capacitors shown in the figure (not necessarily in order). Find the capacitance of a single capacitor which can replace the combination and store the same charge (as the combination).
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We just have to find the equivalent capacitance. If we replace the topmost row by C', C ′ = C 1 1 + C 2 1 + C 3 1 + C 4 1 + C 5 1 1
(Because, C 1 , C 2 , C 3 , C 4 , C 5 are in SERIES.)
C ′ = C 2 C 3 C 4 C 5 + C 1 C 3 C 4 C 5 + C 1 C 2 C 4 C 5 + C 1 C 2 C 3 C 5 + C 1 C 2 C 3 C 4 C 1 C 2 C 3 C 4 C 5
C ′ = α 2 α 3 α 4 α 5 + α 1 α 3 α 4 α 5 + α 1 α 2 α 4 α 5 + α 1 α 2 α 3 α 5 + α 1 α 2 α 3 α 4 α 1 α 2 α 3 α 4 α 5
C ′ = e / a f / a = e f
(USING VIETA'S FORMULA)
Now, C ′ , C 5 , C 4 , C 3 , C 2 , C 1 are in PARALLEL.
So, C e q u i v a l e n t = C ′ + C 5 + C 4 + C 3 + C 2 + C 1
C e q u i v a l e n t = C ′ + [ C 5 + C 4 + C 3 + C 2 + C 1 ] = e f + a b
(USING VIETA'S FORMULA)
Note: In the 3rd step, I have replaced C 1 by α 1 , C 2 by α 2 and likewise, but, it is not necessary that C 1 = α 1 , C 2 = α 2 and so on. Even then, the expression will evaluate to C ′ = product of roots / sum of product of roots taken 4 at a time.