5x5 lattice resistor problem. What is product of most common voltage and number of such nodes?
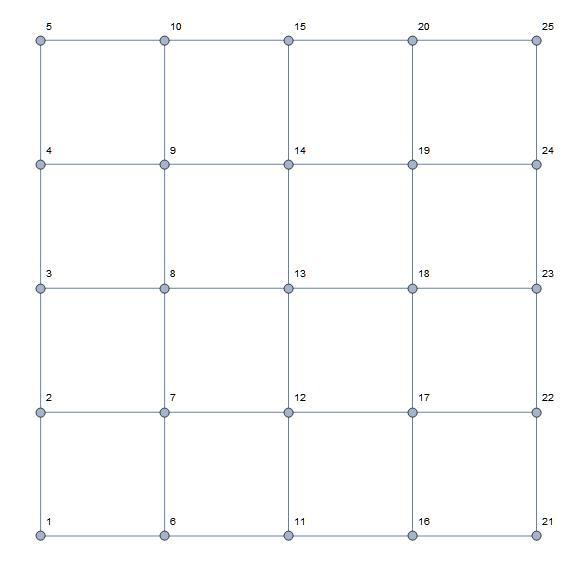
All resistors are 1 .
Positive 3 Volts is applied to node #2. Node #24 is grounded, that is, it is at 0 Volts (connected to the negative connection of the power source).
Each node is at some voltage with respect to ground, e.g., node #2 is at 3 Volt and node #24 is at 0 Volts.
One voltage occurs more often than any of the others. Multiply the number of nodes at that voltage times the voltage at those nodes. That product is this problem's answer.
The answer is 4.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are 3 nodes at 1.5 volts. The product is 4.5.
The vertex labels are: above: the vertex number, below and to the left is the node's effective resistance from node #2 and below and to the right is the ground relative voltage at the node. The edge labels are the differential voltage between the nodes at each end, assuming that the lower numbered node is more positive than the higher numbered node. If the assumption is incorrect, then a negative differential voltage is shown. The nodes with the most common volttage are larger. The nodes are rainbow colored from red (3V) to violet (0V).