6 circs in a hex
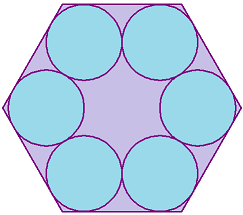
This is the smallest regular hexagon that can pack 6 circles. If the circles are unit circles, find the side length of the hexagon.
The answer is 3.154700538.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
nyc soln. sir!
By symmetry, the radii of the 6 unit circles can be joined to create a smaller regular hexagon with sides of 2 .
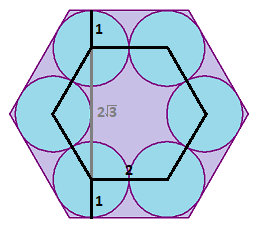
The height h of a regular hexagon with side s is h = 3 s , so the height of the smaller regular hexagon is 2 3 .
Through proportions of the sides and heights of the two similar regular hexagons we have 2 x = 2 3 2 + 2 3 which solves to x ≈ 3 . 1 5 4 7 0 0 5 3 8 .
2 ( 1 + 3 1 ) = 3 . 1 5 4 7 0 0 5 3 8 . . .
B G = D E = 2 . B D = 1 . △ B C D is a 30-60-90 so C D = E F = 3 / 3 .
So one side of the hexagon C D + D E + E F = C F = 2 + 2 3 / 3 ≈ 3 . 1 5 4 7