6 Different Angles
What is the sum of the 6 blue angles?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
49 solutions
I am not convinced that the pink triangle is an equilateral triangle. since there are no parallel lines here. But since it is the SUM of its angles which is important, and since this will always equal 180 degrees, it doesn't matter whether it is or not. John Oakes
Log in to reply
Right, we do not need the assumption that the pink triangle is equilateral :)
I didn't understand anything of your solution.
Log in to reply
Do you understand what the sum of angles of a pink triangle are? Do you see why it gives us 2 of the blue angles and 1 of the angles in the green triangle?
You took the words right out of my mouth! :)
It doesn't matter if the inner triangle is equilateral. It could have been 40, 60, 80, or whatever It would still be one of each of the triangle's angles for them to each add up to 180 and so the inner one does as well.
The sum of all the angles within a triangle (any type) is 180°. The triangle created by the intersection of the three triangles is an equilateral triangle (each angle is the same), so 60°. So 180°+180°+180°-60°-60°-60°= 360°
Makes sense?
Log in to reply
It need not be true that the small pink triangle is equilateral. The result is still true, as John mentioned.
In all there are 3 big triangles & 1 small triangle at the centre.
Sum of measure of angles of all 3 triangles = 180º + 180º + 180º = 540º
But the small triangle at the centre too measures - 180º
(This small triangles has 3 acute angles of the larger triangles)
Thus, Sum of 6 blue angles = 540º - 180º = 360º
Ans. 360º
Nice! That feels so quick :)
Great solution!

3x180 -180=360 Here is how:
BLUE+RED=540
RED=180
BLUE=540-180=360
When traversing the diagram, you turn a total of two revolutions, or 7 2 0 ∘ , before returning at the starting point. This is the sum of the external angles. Since internal angle = 1 8 0 ∘ − external angle , and there are six internal angles here, we have ∑ internal angle = ∑ 1 8 0 ∘ − ∑ external angle = 6 × 1 8 0 ∘ − 7 2 0 ∘ = 3 6 0 ∘ .
I like this too! So many nice ways to view this problem :)
?????? not understood
Turtle Geometry by Abelson and diSessa is a wonderful book - where taught now I wonder?
With a physical straightedge or mental one you can just traverse/pivot on the outer angles and get 360 without even thinking about the inner angles. In all honesty I think it's more fun/easier to just pivot on the relevant angles.
I think you could also consider the angle a vector moving around the path would rotate through to get back to the start.
I held my pen above the line at the right hand side of the diagram. I then rotated it through the acute angles at the top right, bottom left, bottom right, top left, middle left and middle right of the diagram so that after each rotation the pen lined up with another line of the diagram. After passing through all the angles, the pen came back to its original position, having made one complete rotation of 3 6 0 ∘ .
You can gain some confidence in this method by using it to show that the sum of the angles in a triangle is 1 8 0 ∘ and in a quadrilateral is 3 6 0 ∘ .
I like the "rotate a pen" idea!
3X360=540 (3 large triangles) 540 - 180 (common small triangle) = 360
Outer angles = (180 - x) + (180 - y) + (180 - z)
x + y + z = 180
Therefore,
(3 X 180) - 180 = Answer
540 - 180 = 360
360, perfect triangle in the middle which means, 180/3=60. so 180 degrees per triangle minus 60 = 120. which means per triangle has a remaining angle of 120. 120*3= 360 degrees.
Well done :)
Just because it 'looks like' an equilateral triangle does not mean that it is one absolutely. Therefore, none of the angles in the diagram is absolutely determined. Regardless, the sum of the angles of the central triangle is still 180 degrees.
3(big triangles) x 180 = 540
1(small middle triangle) = 180
Deducting the sum of angles from the middle triangle will give you the sum of the 6 angles.
540 - 180 = 360
Well done :)
That's how I did it too (but without the first calc) - err, (3-1) x 180 = 360.
There are three triangle. The sum of the angles inside a triangle is 180. 3 x 180 = 540. The sum of the non blue angles is 180. Therefore 540 - 180 = 360
the sum of all 3 triangles angles is 540, and you know that 3 of thoes angles are not accounted for, so it must be 540-180=360
Although the diagram 'looks' like a solution, do we really know that the sides will make a quadrilateral after flipping?
180=180-ang1'-ang2'+180-ang1''-ang2''+180-ang1'''-ang2''' ----- 3*180-180= sum angles
Oh, that's a nice equation to put together!
the sum of all angles in three triangles =3*180, and the 6 angles represent that sum -the sum of angles in the small triangle which is equal 360
Nice! That's what I did too :)
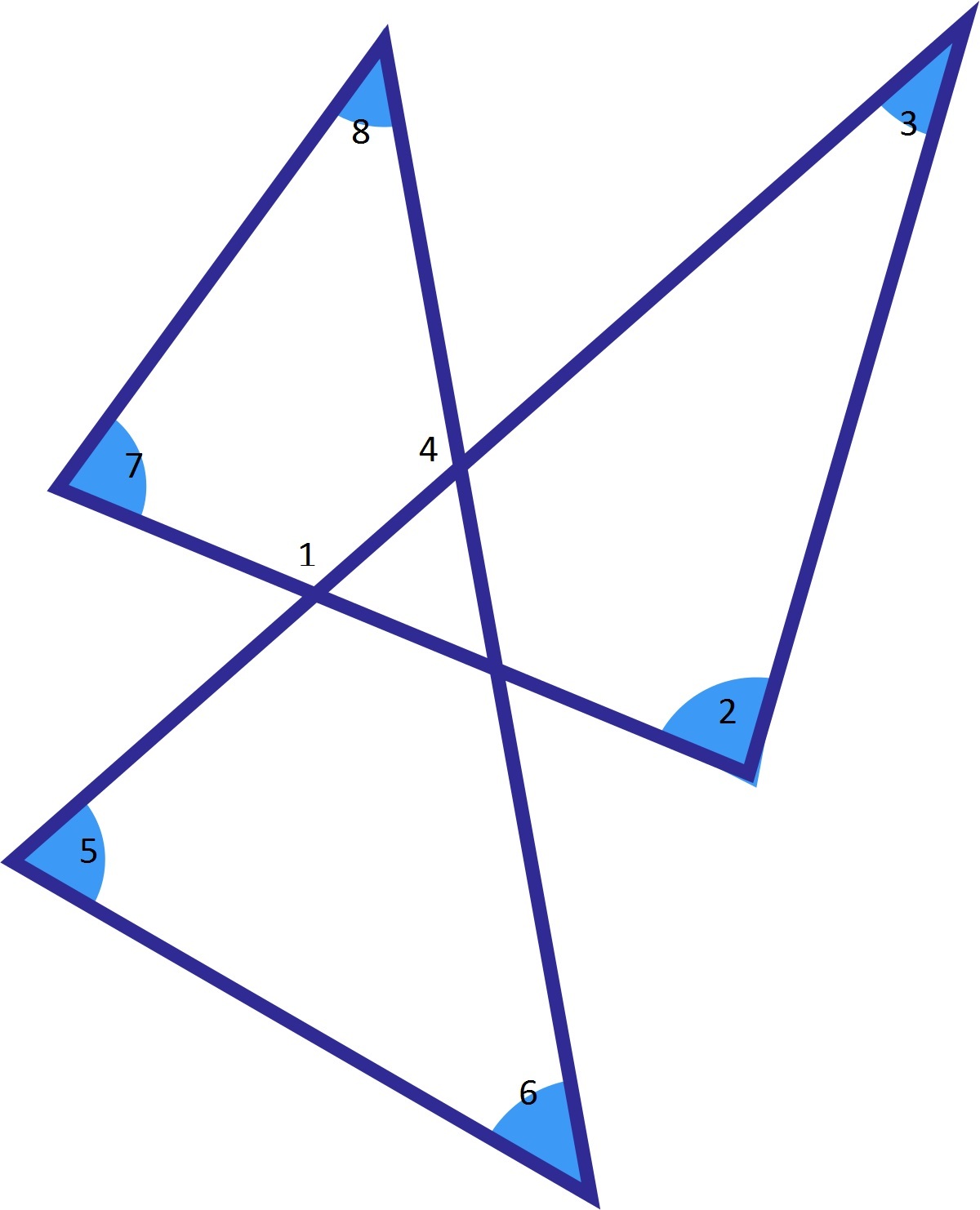 Angle 1 = Angle 2 + Angle 3 (Exterior Angles of a triangle equal the sum of the 2 remote interior angles)
Angle 1 = Angle 2 + Angle 3 (Exterior Angles of a triangle equal the sum of the 2 remote interior angles)
Angle 4 = Angle 5 + Angle 6 (Exterior Angles of a triangle equal the sum of the 2 remote interior angles)
Angle 1 + Angle 4 + Angle 7 + Angle 8 = 360° (The sum of the interior angles of any 4 sided polygon equals 360°)
Angle 2 + Angle 3 + Angle 5 + Angle 6 + Angle 7 + Angle 8 = 360° (Substitution)
Nice way of presenting it!
Imagine walking along the lines. You walk, turn, walk, turn again in the same direction, walk, turn again in the same direction etc. If you end up back where you started then one way or another you’ve gone in a circle. (360deg).
central triangle is an equilateral, thus each angle is 60°. Each central triangle's angle is also an angle of the other 3 triangles. Thus an easy subtraction gives you the answer.
Apply the Exterior Angle Theorem for a triangle twice, then use the fact that the sum of the measures of the angles of a quadrilateral is 360. Easy!
Sum of the three large triangles (3*180) minus sum of the small inner triangle formed (180)
Because the angles encompass the exterior angles- it is effectively the pie pieces cut out of a hypothetical circle. They have to be 360 degrees, a complete boxing of the compass.
The shape is made of 3 triangles - seperate these triangles and the sum of all the angles is 3 x 180 = 540 deg when we overlap the triangles again we get a smaller triangle created - this is made up of 3 of the previous angles. the small triangle angles add up to 180 degrees - so we subtract this from the total so 540 -180 = 360 QED
3 180 = sum of angles in triangles with blue angles, that sum includes sum of angles of their intersections which is 180, therefore (3-1) 180 = 360
Visualize 3 triangles intersecting (two of the blue angles and a third unshaded). Starting with triangle in top left and moving clockwise you have triangle abC, deF, & ghI (lower case are shaded blue, upper case is not). From basic geometry we know the 3 angles of each triangle add to 180.
Start with the triangle in the top left. Label its angles a, b, & C. Angle C is created from two intersecting lines. Either of the adjacent angles is equal to 180 - [C]. Naturally this adjacent angle must be equal to the sum of two shaded angles of the triangle, (that is, a+b).
Notice now that you have a quadrilateral in bottom left: it has angles g & h, as well as the angle a+b that you derived, and finally a fourth angle yet undetermined. This fourth angle can be determined similarly to the 180 - [C] = (a+b) angle we derived and it is found to be d+e.
So we are left with a quadrilateral that has the four angles: g, h, (a+b), & (d+e). Like a triangle's angles add up to 180, a quadrilaterals add to 360. Therefor g + h + (a+b) + (d+e) must equal 360.
Each angle of the three outer triangles are equal to one angle of a triangle next to it. And to one angle of the small interior triangle. So basically it's 180 × 2, because each angle degree appears twice.
Each of the three large triangles has angles adding to 180, of course, so the six blue angles plus the three angles of the center triangle add up to 3x180. But the center triangles' angles add up to 180, so the sum of the blue angles is 2x180, or 360.
Each triangle sums to 180 degrees. So, for each triangle, simply represent the sum of the blue angles with a variable and solve for the third angle: 1) A1 = 180 - A. 2) A2 = 180 - B. 3) A3 = 180 - C.
Keep in mind that the Sum A+B+C represents the sum of all blue angles.
Also notice that these three angles are part of the smaller, center triangle, so their sum total has to be 180 degrees:
A1+A2+A3 = 180,
Giving us:
540 - (A+B+C) = 180,
Which after simplification gives:
A+B+C = 360
Thus the total value represented by the three angles is 360 degrees.
There are three overlapping Triangles 1, 2, and 3 . Consider 1 with marked angles 1 and 2 with Apex angle =x, therefor x=180 - (1+2 ) Hence (1+2) = 180-x . Similarly (3+4)=180-y and (5+6)=180-z Add these three to give (1+2) +(3+4) +(5+6)= 3x180-(x+y+z), But (x+y+z) = 180 therefor (1+2)+(3+4)+(5+6)=(3x180)-180=2x180 =360
Twist the shape to a rectangle. And we all know rectangle is 360
regardless of starting point in order to return to starting point one must go a full circle so to speak
sum of 1 triangle is always 180 degrees, multiplied by 2 is 360
If we call the angle of the internal angles of the small triangle a,b and c, and consider the fact that the internal angles of a triangle are 180 degrees, we then have 180-a+180-b+180-c=180x3 - (a+b+c). a+b+c=180, so the sum of the 6 blue angles is 180x3-180=360
Let a1,b1,c1 be the angles of triangle1, a2,b2,c2 for triangle 2, and a3,b3,c3 of triangle3, where c1,c2,c3 are angles of the smaller intersecting triangle 4.
- Step 1a) c1+c2+c3=180.
- Step 1b) c1=(180-(a1+b1)) c2=(180-(a2+b2)) c3=(180-(a3+b3))
- Step 2) (180-(a1+b1))+(180-(a2+b2))+(180-(a3+b3))=c1+c2+c3=180
- Step 3) 180-a1-b1+180-a2-b2+180-a3-b3=180
- Step 4) 180+180+180-180=a1+b1+a2+b2+a3+b3
- Step 5) 360 = a1+b1+a2+b2+a3+b3

Small triangle sum of angles: a + b + c = 1 8 0
Upper left triangle: 1 8 0 − ( α + β ) = a
Upper right triangle: 1 8 0 − ( γ + δ ) = b
Lower triangle: 1 8 0 − ( ϵ + ζ ) = c
Now, ( ( 1 8 0 − ( α + β ) ) + ( ( 1 8 0 − ( γ + δ ) ) + ( ( 1 8 0 − ( ϵ + ζ ) ) = a + b + c = 1 8 0
Solving for ( α + β ) + ( γ + δ ) + ( ϵ + ζ ) yields 360.
The sum of each triangle's angle is 180 degrees. The small triangle formed by the intersection of the three triangles is an equilateral triangle where all angles are 60 degrees. (180-60)3 = (120)3 = 360
The small triangle need not be equilateral. We're still subtracting off all of the angles, so we have 3 × 1 8 0 − 1 8 0 = 3 6 0 .
The sum of the angles of a triangle is 180 degrees The triangle with no blue angles is made of the non blue angle of each of the other three triangles If their sum (180) is subtracted from the sum of the other tree (540) the result is 360
You have two right triangles on the upper left and upper right.The lower angles have to be 90 degrees. The bottom triangle is an equalateral triangle so the two marked angles have to be 45 degree. So far that is 90 X 2 +45 X 2 which is 270 degrees. A simple observation of the legs on the upper right triangle show that the short one is half as long as the long one so the marked angle is 30 degrees.We are now up to 300 degrees worth of marked angles. The left upper triangle's remaining marked angle is twice as big as the one on the right therefore it has to be 60 degrees and the final answer is 360 degrees. Besides if you take all the blue markings out and place them together flat edge to flat edge they make a perfect circle and guess what, voila 360 degrees.
Let's assign labels to each of the angles:

The sum of A, B, and C is 180 degrees. Same goes for angles D, E, and F, as well as angles G, H, and I.
A + B + C = 180
D + E + F = 180
G + H + I = 180
So now we can calculate the sum of all the angles:
(A + B + C) + (D + E + F) + (G + H + I) = X
But we only want the blue shaded ones. So we have to remove the three angles that make up the smaller, center triangle:
(A + B + C) + (D + E + F) + (G + H + I) - (A + D + G) = X
We don't know the actual values of A, B, C, or any of the angles, but we do know what they add up to for each triangle - 180 degrees. Each triangle is represented by the grouping right able, so substituting 180 for each group, we get:
180 + 180 + 180 - 180 = X
And then it's simple addition and subtraction from there:
180 + 180 + 180 - 180 = 360
Taking any one side, it is effectively turning through 360, albeit displaced and extended.
i saw it as 2 triangles in my head and figured 180 degrees in each triangle times 2
There are three large triangles each at 180 degrees, one angle of each provides an angle to the smaller internal triangle also required to add up to 180 degrees. Therefore 3 x 180 = 540. 540 - 180 = 360. They remaining 6 angle must add up to 360 total degrees.
3*180 -(x+y+z) , x+y+z = 180, 2(180) = 360
middle is an equilateral triangle, each internal angle of middle triangle completes 3rd corner of a triangle with two blue angles, therefore sum of each pair of blue angles = 120
What makes you believe that the middle triangle is an equilateral triangle? It isn't forced to be.
Log in to reply
It actually doesn't matter what type of triangle it is, since it still has the same sum of internal angles, each of which completes one of the larger triangles. So it will always be (180*3) - 180 = 360 regardless of how the internal angles of the middle triangle are distributed.
Log in to reply
Agree with that. The bit about the sum of each pair of blue angles being 120 degrees is (I think) incorrect
Each angle has a complementary one such that if we move a corner along one of the three 'long lines', its complementary angle changes such that the sum of the two is constant. Thus, moving a corner in such a way, we keep the sum of the angles constant. It is trivial to move points around like this such that the lines form two triangles on top of each other at the centre (the small triangle we see already). Thus, the angles sum to twice the sum of the angles in a triangle: 360 degrees.
Of course, we never appealed to the specific case shown, so in fact one could move any points around however one likes in order to construct a 'double triangle' and the result would still hold.
Nice interpretation :)
All of the triangles can be seen as one contigious figure if they are seen to be connected by one continous line, and the sum of the angles in any contigious figure is always 360 degrees.
The sum of the internal angles of a triangle is 180 ((3-2) 180). The smallest triangle contains the three angles missing from each of the "larger" triangles. Therefore the sum is 3 180 (for the three larger triangles) -180 (the sum of the missing angles formed by the smallest triangle. Or 540-180=360 degress

From the diagram, we see that
1 + 2 + C = 180
3 + 4 + A = 180
5 + 6 + B = 180
A + B + C = 180
Now from the above equations, we see that
1 + 2 + 3 + 4 + 5 + 6 = 180 + 180 + 180 - (C + A + B) = 180 * 3 - 180 = 360
Another way:
Rotate line XY clockwise through all the angles in the following sequence: 2 5 6 3 4 1. The line made one complete revolution; so the sum of those angles is 360.
The sum of the angles in a triangle is always 180, so the measure of all the angles of all the triangles would be 180x3=540. BUT! We aren't counting the angles that fall inside the little central triangle, which (since they themselves form a triangle) add up to 180. Thus, the answer is 180 x 2 = 360!
there are three big triangles and one small then small triangle is an Equilateral triangle so all the big triangles having miss an angle of 60...... so 120+120+120=360
We are asked to be creative. Unfold the drawing and you see a rectangle. In doing so, six angles "become" four angles....four corners angles of a rectangle: 90 + 90 + 90 +90 = 360. Just sayin'.
I "unfolded" the diagram and made a rectangle. a rectangle has a total of 360 degrees
Is the middle triangle an equilateral triangle? How do you know?
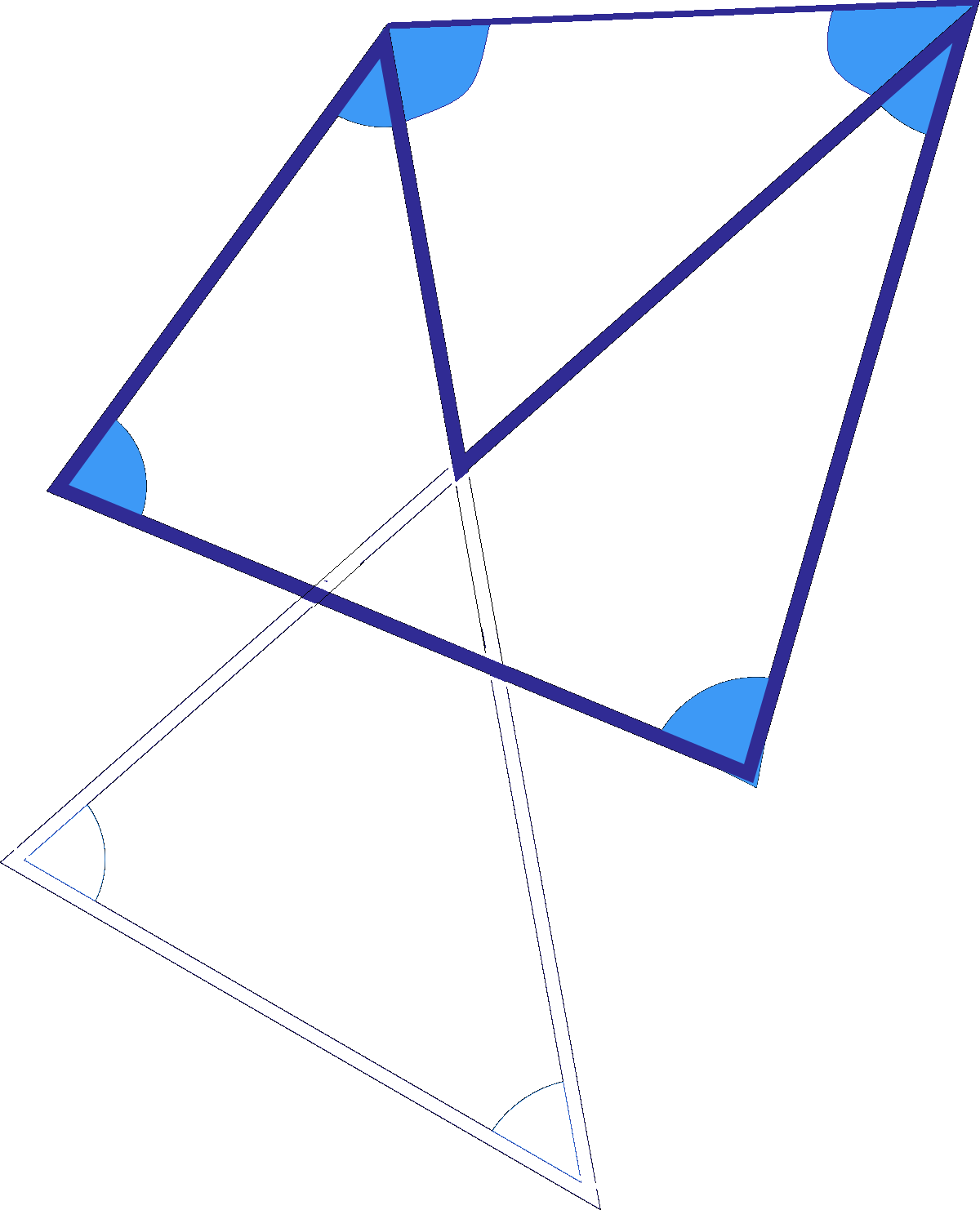
The blue angles are equal to the sum of the angles in the 3 pink triangles, minus the sum of the angles in the green triangles. Hence, the sum is
3 × 1 8 0 ∘ − 1 8 0 ∘ = 3 6 0 ∘