60°- 30° right triangles

${\color{#D61F06} R_{length}} = \sqrt{2^{2} + \sqrt{3}^{2}} = \sqrt{7}$ Set up the equations: $\begin{aligned} & {\color{#D61F06} (1)}~y = -\frac{\sqrt{3}}{2}x + \frac{3\sqrt{3}}{2} \\ & {\color{#333333} (2)}~y = \frac{\sqrt{3}}{5}x. \end{aligned}$ Find the point of intersection: $\begin{aligned} \left ( \frac{\sqrt{3}}{5} + \frac{\sqrt{3}}{2} \right )x &= \frac{3\sqrt{3}}{2} \\ \frac{7\sqrt{3}}{10}x & = \frac{3\sqrt{3}}{2} \\ \frac{7}{5}x & = 3 \\ x &= \frac{15}{7} \\ \implies y &= \frac{3\sqrt{3}}{7}.\end{aligned}$ Now, you have: ${\color{#3D99F6} B_{length}} = \sqrt{\left ( \frac{15}{7}-2 \right )^{2} + \left ( \frac{3\sqrt{3}}{7}\right )^{2}} =\sqrt{\frac{28}{49}} = \frac{2\sqrt{7}}{7}.$ Hence, $\frac{{\color{#D61F06} R_{length}}}{{\color{#3D99F6} B_{length}}} = \dfrac{\sqrt{7}}{\frac{2\sqrt{7}}{7}} = \frac{7}{2} = \boxed{3.5}.$

Relevant wiki: Cosine Rule (Law of Cosines)

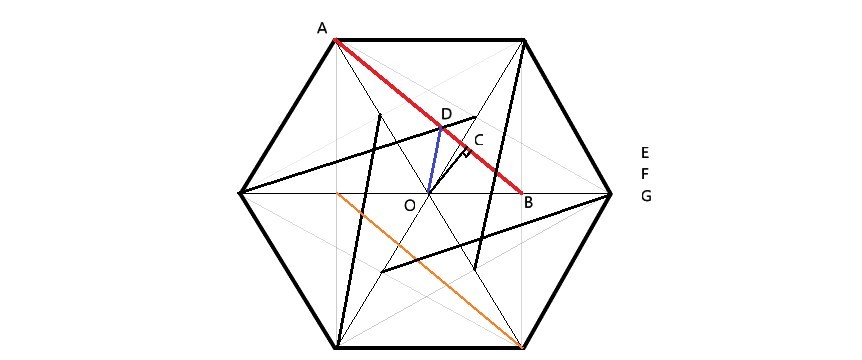
We expand the graph into a complete hexagon, and found that the six linked segment construct another smaller inside hexagon.

Let $AO = 2$ so then $OB = 1$ , using Law of Cosine obtain $AB = \sqrt{7}$ .

Using different area expressions of $\Delta AOB$ , yield

$AO \times OB \sin{120^\circ} = AB \times OC$ then get $OC = \sqrt{\frac{3}{7}}$ .

Let's observed closer at the smaller hexagon, we have $OD \cos{30^\circ} = OC$ and gives us $OD = \frac{2}{\sqrt{7}}$ .

Finally, the ratio of the red segment's length to the blue segment's length will be $\frac{AB}{OD} = \boxed{\frac{7}{2}}$ .

(my English is poor) i use the axis to solve it ,may be using the geometric is more good)

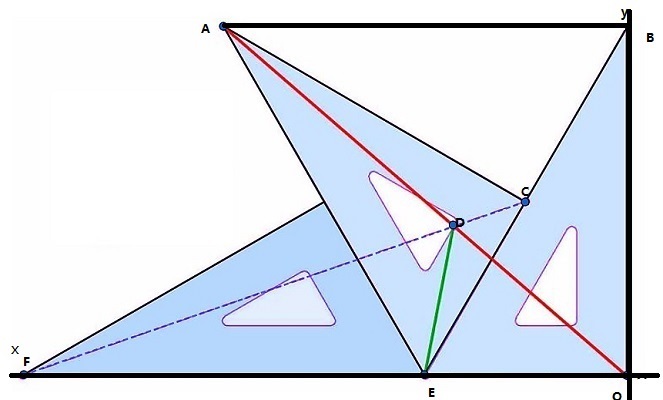
my method: 1:calculate AO (use AB and BO)
2:determine the equation of AO
3:determine the equation of DE
4:determine the coordinate of D and E
5: calculate the length of DE
END

|3 is the square root of 3
- assume EO=1 BO=|3

so AC=|3 EC=1
EB=2
so cb=1
∠ACB = 90
so AB=2 and ∠ABO=90
A(2，|3)
AO=|7
AO is y= $\frac{|3}{2}$ x
C is the midpoint of EB
C ( $\frac{1}{2}$ , $\frac{|3}{2}$ ）
F(3,0)
so FC is y=- $\frac{|3}{5}$ x + $\frac{33}{5}$

then D ( $\frac{6}{7}$ , $\frac{3|3}{7}$ ）
DE= $\frac{2|7}{5}$

the Ans is 3.5

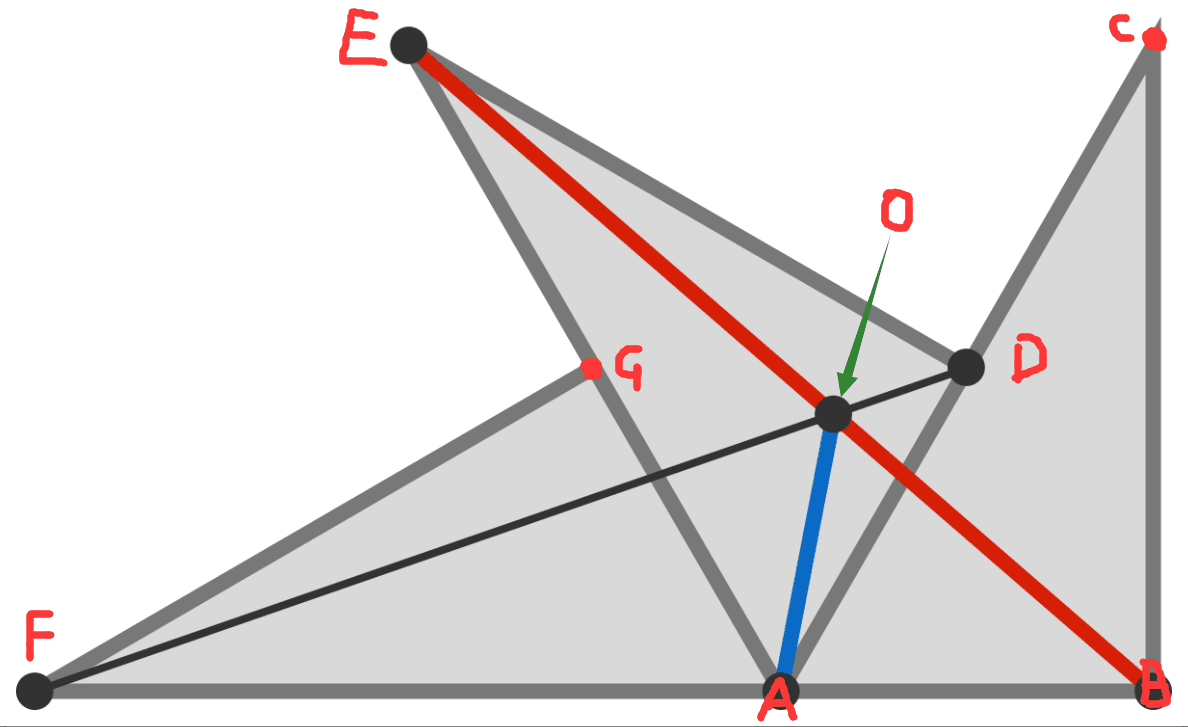We can prove that △BOF is similar to △AOE and △DOA. So the ratio of OB to OA is the same as the ratio of BF to AE, which is actually 3:2. Also, the ratio of OA to OE is the same as the ratio of AD to AE, which is actually 2:1. So, the ratio of BE and OA is 3.5

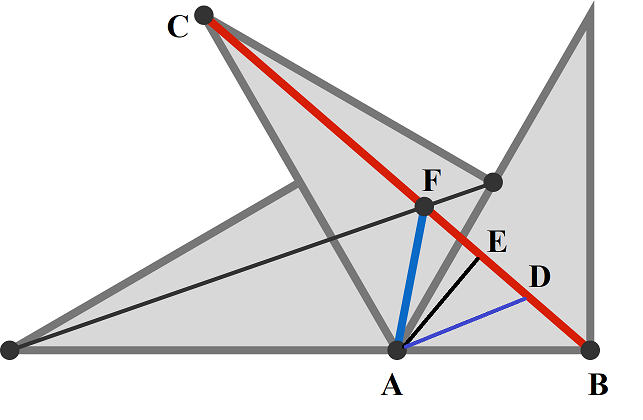
Denote $a=AB$ , $b=BC$ , $c=AF$ , $h=AE$ . There follows $AC=2a$ , $\angle CAB=\dfrac{2\pi}3$ . Applying the cosine theorem, we find $b=a\sqrt7$ . Denote $s=\dfrac{a+2a+b}2=\dfrac a2(3+\sqrt7)$ and apply Heron's formula to find the area of $\Delta ABC$ , obtaining $\dfrac{a^2\sqrt3}2$ . On the other hand the area of $\Delta ABC$ is $\dfrac{bh}2=\dfrac{ah\sqrt7}2$ , so $h=a\sqrt{\dfrac37}$ . Taking into account that the triangle $ADF$ is equilateral, with $c=AF=AD=DF$ , and its area is $\dfrac{c^2\sqrt3}4=\dfrac{ch}2=\dfrac{ca}2\sqrt{\dfrac37}$ . So $c=\dfrac{2a}{\sqrt7}$ , and the required ratio is $\dfrac bc=\dfrac{a\sqrt7}{\dfrac{2a}{\sqrt7}}=\dfrac72=3.5$ .

Sorry，I'm just not good at English.So I decided to draw a picture to show the solution.

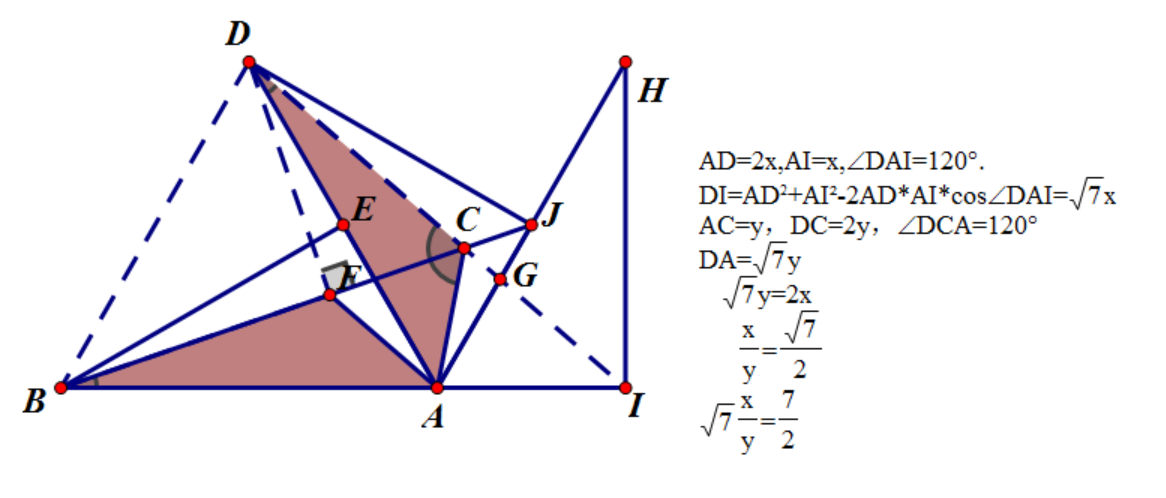
TLDR;

${\color{#D61F06} R}=\sqrt{2.5^{2}+{\frac{\sqrt{3}}{2}}^{2}} = \sqrt{7}$

$\Delta AEC similar \Delta ACD$

$\frac{\sqrt{7}}{2}*\frac{\sqrt{7}}{1}=3.5$

I thought this was a rather elegant solution, but I could not find a way to prove $\Delta AEC$ is similar to $\Delta ACD$ in a simple way

1. Since all three 30-60-90 triangles are the same the red line is the same as the black line. $\Delta AEC = \Delta FBC$
2. The triangle ABC we know because it is a 30-60-90 triangle its sides are $AB=\sqrt{3}$ , $AC=2$ , and $BC=1$ (or any multiple) segment $BC=1$ and segment $GC=2$ . We know $BC$ is half way between segment $CE$ and segment $GE$ so the dimensions of $\Delta BFH$ are $2.5,\sqrt{3}/2$
3. Solve for the black and red line $\Delta AEC = \Delta FBC$ ${\color{#D61F06} R}=\sqrt{2.5^{2}+{\frac{\sqrt{3}}{2}}^{2}} = \sqrt{7}$ Now we know $\Delta AEC$ 's sides $AC=2,CE=1,AE=\sqrt{7}$
4. We can determine $\Delta AEC$ is similar to $\Delta ACD$ Recognizing $\angle FDE$ is the interior angle of a regular hexagon $\angle FDE=120$ ToDo (please help)
5. Given $\Delta AEC$ is similar to $\Delta ACD$ we set up the proportion of the larger triangle $AE$ to the smaller triangle $AC$ and the proportion of the longest side $AE$ to the shortest side $CE$ .

$\frac{\sqrt{7}}{2}*\frac{\sqrt{7}}{1}=3.5$

open autocad on your computer, draw 30 60 triangle, copy it and rotate 60 degrees, draw the additional needed lines and get thier, dimentions, after dividing them by each other you will get the ratio 3.5:1 ... No clapping. Thank you.

the blue segment can be seen a side of the equilateral triangle that lies on the red segment