600,000 Points Problem

Calculus Level 5

If I 1 = ∫ 0 ∞ s i n x x d x \displaystyle{I_{1}=\int^{\infty}_{0}\dfrac{sinx}{x} dx} and I 2 = ∫ 0 ∞ s i n 3 x x d x \displaystyle{I_{2}=\int^{\infty}_{0}\dfrac{sin^3x}{x} dx}

Now say k k be, k = I 1 I 2 k=\dfrac{I_{1}}{I_{2}} .

Let following summation be S S . S = ∑ n = 1 ∞ 7 n . 6 n ( 7 n − 6 n ) . ( 7 n + 1 − 6 n + 1 ) \displaystyle{S=\sum_{n=1}^{\infty}\dfrac{7^n.6^n}{(7^n-6^n).(7^{n+1}-6^{n+1})}}

If a reaction from reactant A A to product B B have 1st order forward rate constant K K and first order backward rate constant(from B back to A) K − 1 K_{-1} .

A ⇌ B \ce{A} \ce{<=>} \ce{B}

Find the concentration of B(in M)= j j after long time, if the initial concentration [ A ] o = 1 M [A]_{o}=1 M and K = 1 s e c − 1 K=1 sec^{-1} and K − 1 = 2 s e c − 1 K_{-1}=2 sec^{-1} . (Take initial concentration of B to be 0)

Input k × j × S k \times j \times S


The answer is 4.

Md Zuhair by Md Zuhair , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Mark Hennings
May 20, 2019

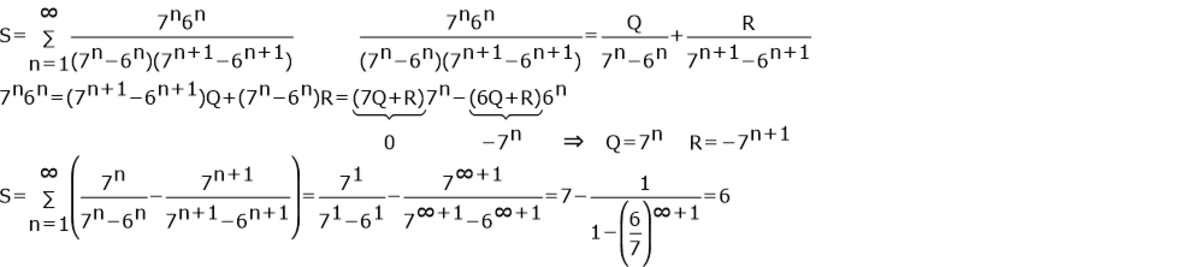
To begin with, I 1 = ∫ 0 ∞ sin ⁡ x x d x = ∫ 0 ∞ sin ⁡ 3 x x d x = ∫ 0 ∞ 3 sin ⁡ x − 4 sin ⁡ 3 x x d x = 3 I 1 − 4 I 2 I_1 \; = \; \int_0^\infty \frac{\sin x}{x}\,dx \;=\; \int_0^\infty \frac{\sin 3x}{x}\,dx \; =\; \int_0^\infty \frac{3\sin x - 4\sin^3x}{x}\,dx \; = \; 3I_1 - 4I_2 so that I 1 = 2 I 2 I_1 = 2I_2 , and hence k = 2 k=2 .

Since 6 n × 7 n ( 7 n − 6 n ) ( 7 n + 1 − 6 n + 1 ) = 6 n 7 n − 6 n − 6 n + 1 7 n + 1 − 6 n + 1 \frac{6^n \times 7^n}{(7^n - 6^n)(7^{n+1} - 6^{n+1})} \; = \; \frac{6^n}{7^n - 6^n} - \frac{6^{n+1}}{7^{n+1} - 6^{n+1}} we deduce that ∑ n = 1 N 6 n × 7 n ( 7 n − 6 n ) ( 7 n + 1 − 6 n + 1 ) = 6 − 6 N + 1 7 N + 1 − 6 N + 1 \sum_{n=1}^N \frac{6^n \times 7^n}{(7^n - 6^n)(7^{n+1} - 6^{n+1})} \; = \; 6 - \frac{6^{N+1}}{7^{N+1} - 6^{N+1}} for any N N , and hence S = 6 S = 6 .

Finally, the differential equation − d [ A ] d t = [ A ] − 2 ( 1 − [ A ] ) = 3 [ A ] − 2 -\frac{d[A]}{dt} \; = \; [A] - 2(1-[A]) \; = \; 3[A] - 2 or d [ A ] d t + 3 [ A ] = 2 \frac{d[A]}{dt} + 3[A] \; = \; 2 with the initial condition [ A ] ( 0 ) = 1 [A](0) = 1 , has the solution [ A ] = 2 3 + 1 3 e − 3 t [A] \; = \; \tfrac23+ \tfrac13e^{-3t} and so the concentration of B B is [ B ] = 1 − [ A ] = 1 3 − 1 3 e − 3 t [B] \; = \; 1-[A] \; = \; \tfrac13 - \tfrac13e^{-3t} which converges to j = 1 3 j=\tfrac13 as t → ∞ t \to \infty .

Thus k × j × S = 2 × 6 × 1 3 = 4 k \times j \times S \,=\, 2 \times 6 \times \tfrac13 \,=\, \boxed{4} .

6 Helpful 2 Interesting 3 Brilliant 1 Confused
Iliya Hristov
Feb 29, 2020

2 Helpful 1 Interesting 1 Brilliant 0 Confused

Iliya Hristov - 7 months, 3 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...