640 math puzzles - 6 Mrs. Miniver’s Problem
The problem derives from "A Country House Visit", one of Jan Struther's newspaper articles featuring her character Mrs. Miniver. According to the story:
She saw every relationship as a pair of intersecting circles. It would seem at first glance that the more they overlapped the better the relationship; but this is not so. Beyond a certain point the law of diminishing returns sets in, and there are not enough private resources left on either side to enrich the life that is shared. Probably perfection is reached when the area of the two outer crescents, added together, is exactly equal to that of the leaf-shaped piece in the middle. On paper there must be some neat mathematical formula for arriving at this; in life, none.
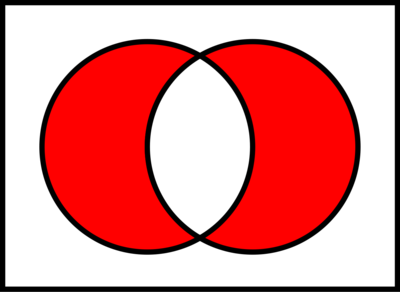
That is to say, given two circles with radius r , find the distance d between the two centers so that the inner intersection area equals the sum of the outer area (red).
Submit ⌊ 1 0 0 0 0 r d ⌋ .
The answer is 5298.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
If the lens (white) is to equal the two crescents (red), then the lens must be twice the area of one crescent. But since the lens plus the crescent equals one circle, we can say the lens must be 3 2 of the circle.
The area of a lens is given by this formula :
A = π r 2 − 2 r 2 tan − 1 ( 4 r 2 − d 2 d ) − 2 d 4 r 2 − d 2
Let r = 1 and equate to 3 2 of a circle:
π − 2 tan − 1 ( 4 − d 2 d ) − 2 d 4 − d 2 = 3 2 π
Solving numerically , d ≈ 0 . 5 2 9 8 6 4 , or ⌊ 1 0 0 0 0 r d ⌋ = 5 2 9 8
By phone calculator's iterations, I got d = 0.52986417 for r = 1.
Lens area (A) with distance d between two equal circles of unit radius is put equal as 2*pi-2A=A, which gives equation for d as
2Tan⁻¹[d/√(4-d²)]+(d/2)√(4-d²)=(⊓/3)
which is solved using WolframAlpha for distance d between two circles as 0.529864.
Answer = 5298
WolframAlpha find d ≈ 0 . 5 2 9 8 6 4 1 6 9 2 0 5 5 5 4 . . . for r = 1 and answer is 5 2 9 8 .
Since the positions of the two circles are symmetrical about the central vertical line, we need only to consider one circle. Let the radius of the two circles be 1 so that our requirement is to find d , the separation between the two centers, such that A 1 = A 2 . Since A 3 is the reflection of A 1 , A 1 = A 3 , then A 1 = A 2 = A 3 = A . We also note that together A 1 , A 2 , and A 3 form a circle. Therefore A 1 + A 2 + A 3 = 3 A = π ⋅ 1 2 ⟹ A = 3 π .
To find A , we consider A 3 . Let the central angle which extends the segment A 3 be θ . Then we have:
A = A 3 = area of sector 2 θ − area of triangle 2 sin θ = 3 π ⟹ 3 sin θ + 2 π = 3 θ
Solving the equation numerically, we have θ ≈ 2 . 6 0 5 3 3 . And d = 2 cos 2 θ ≈ 0 . 5 2 9 8 5 9 9 9 8 , then ⌊ 1 0 0 0 0 r d ⌋ = 5 2 9 8 .