6th-Order LC Circuit
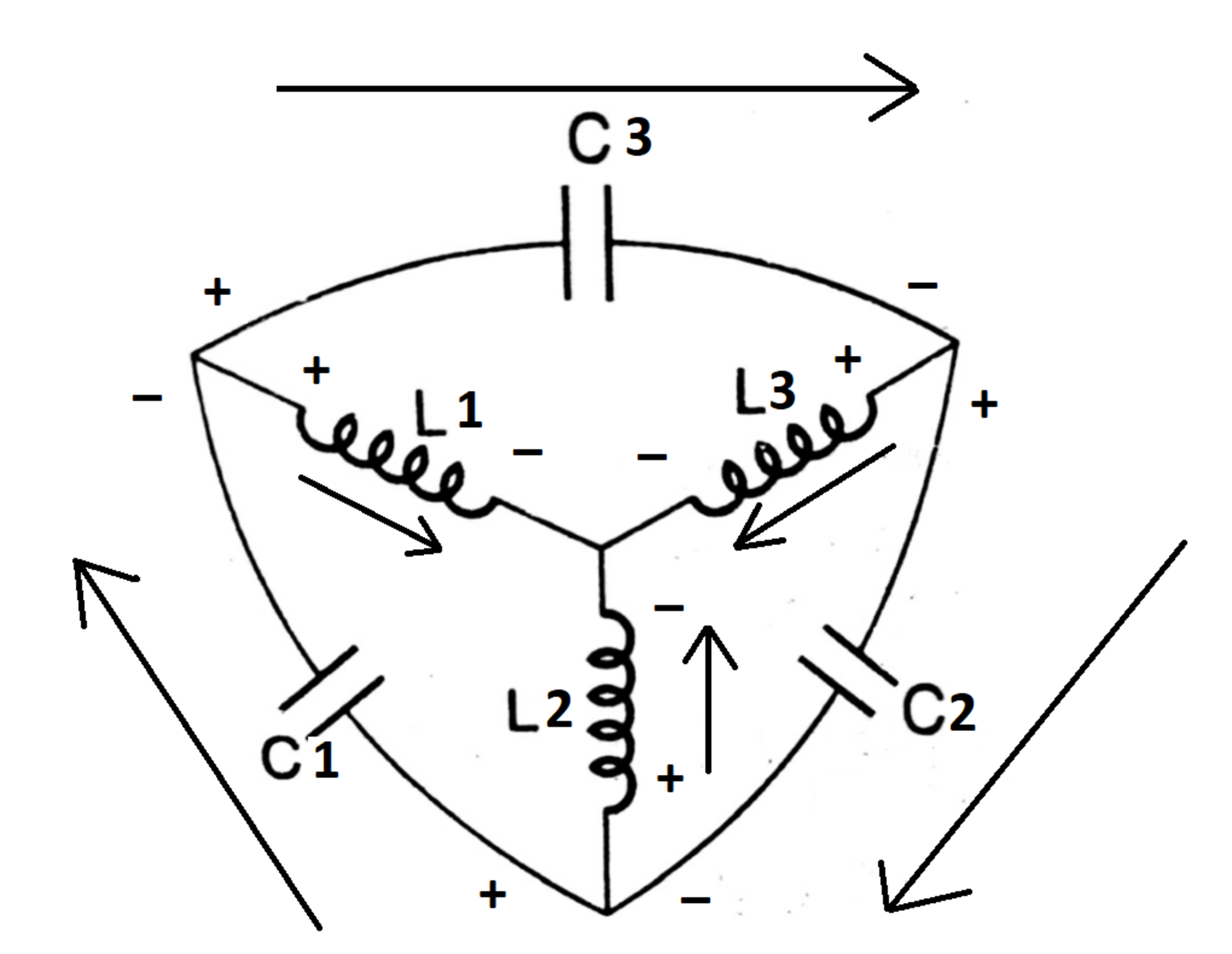
The circuit below consists of three capacitors ( C 1 = 2 , C 2 = 2 , C 3 = 3 ) and three inductors ( L 1 = 2 , L 2 = 3 , L 3 = 1 ) . At time t = 0 the inductor currents are zero and the capacitor voltages are ( V C 1 = + 5 , V C 2 = + 7 , V C 3 = − 1 2 ) .
At time t = 4 , what fraction of the total system energy is contained within the three capacitors combined?
Note: In the drawing, the plus and minus signs indicate voltage polarities, and the arrows indicate current polarities.
The answer is 0.15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath Y E A H ! Everyone is a legend until the real legend comes.
I don't know why why why. But sometimes your solution seems me as an ideal solution for a problem like this one .
Log in to reply
Thank you! Truth is that this solution is not ideal. Solving a 9 equation system is very tedious and time-consuming. I have left out those steps. Deriving a state-space form and numerical integration is a less tedious method to solve this problem.
Writing the loop equations, and using the voltages across the capacitors and the currents through the inductors as our variables, we get,
V C 1 − L 2 d t i L 2 + L 1 d t d i L 1 = 0 ( 1 )
V C 2 − L 3 d t i L 3 + L 2 d t d i L 2 = 0 ( 2 )
V C 3 − L 1 d t i L 1 + L 3 d t d i L 3 = 0 ( 3 )
We now note that
V C 3 = − V C 1 − V C 2 ( 4 )
and, with this last equation, if we add, equations (1) through (3), we get an identity, which implies that one of the equations is linearly dependent on the
other two. So we can eliminate the third equation and the variable V C 3 as it is linearly dependent on V C 1 and V C 2 .
further,
i L 3 = − i L 1 − i L 2 ( 5 )
Substituting this into equation (2),
V C 2 + L 3 ( d t i L 1 + d t i L 2 ) + L 2 d t d i L 2 = 0 ( 6 )
equations (1) and (6) can be solved for d t d i L 1 and d t d i L 2 in terms of V C 1 and V C 2 .
Define the matrix,
L = [ − L 1 − L 3 L 2 − L 2 − L 3 ]
then
⎣ ⎢ ⎡ d t d i L 1 d t d i L 2 ⎦ ⎥ ⎤ = L − 1 [ V C 1 V C 2 ]
Next, we have the following equations,
i C 1 = C 1 d t d V C 1 = i L 1 + i C 3 ( 7 )
i C 2 = C 2 d t d V C 2 = i C 1 + i L 2 ( 8 )
i C 3 = C 3 d t d V C 3 = i L 3 + i C 2 ( 9 )
Using equation (5), which is,
i L 3 = − i L 1 − i L 2 ( 5 )
and again, we can eliminate i L 3 from our variables, as it is linearly dependent on i L 1 and i L 2 . So, we can re-write equation (7) as follows,
C 1 d t d V C 1 = i L 1 − C 3 ( d t d V C 1 + d t d V C 2 ) ( 1 0 )
also, we can write equation (8) as follows,
C 2 d t d V C 2 = C 1 d t d V C 1 + i L 2 ( 1 1 )
The last two equations can be solved for d t d V C 1 and d t d V C 2 in terms of i L 1 and i L 2
Define the matrix C as follows
C = [ C 1 + C 3 − C 1 C 3 C 2 ]
then it follows that
⎣ ⎢ ⎡ d t d V C 1 d t d V C 2 ⎦ ⎥ ⎤ = C − 1 [ i L 1 i L 2 ]
Now we have the system fully specified, so if we define the vector x as follows,
x = ⎣ ⎢ ⎢ ⎡ i L 1 i L 2 V C 1 V C 2 ⎦ ⎥ ⎥ ⎤
Then, the dynamics of the system are given by,
x ˙ = A x , where the matrix A is given by,
A = [ 0 2 × 2 C − 1 L − 1 0 2 × 2 ]
This coupled with x ( 0 ) = [ 0 , 0 , 5 , 7 ] T
This system can be solved using a numerical integration method such as the 4th-order Runge-Kutta method (a widely known method), from t = 0 to t = 4 . The required fraction is computed based on the fact that the energy stored in a capacitor is given by 2 1 C V 2 .
Therefore,
Fraction of Energy = 2 1 C 1 ( 5 ) 2 + 2 1 C 2 ( 7 ) 2 + 2 1 C 3 ( 1 2 ) 2 2 1 C 1 V C 1 2 ( 4 ) + 2 1 C 2 V C 2 2 ( 4 ) + 2 1 C 3 ( V C 1 ( 4 ) + V C 2 ( 4 ) ) 2
This fraction comes out to be about 0 . 1 5 . In summary the dynamics of this circuit is described by a 4-th order differential equation which is implemented using the state space approach by a first order differential equation (with constant coefficients) of the state vector with has dimension 4.
Slightly different approach from that of @Hosam Hajjir
The circuit equation by applying Kirchoff's current and voltage laws read:
Q ˙ 3 = I C 3 Q ˙ 2 = I C 2 Q ˙ 1 = I C 1
I C 3 = I C 2 + I L 3 I C 1 = I C 3 + I L 1 I C 2 = I C 1 + I L 2
C 3 Q 3 + L 3 I ˙ L 3 = L 1 I ˙ L 1 C 2 Q 2 + L 2 I ˙ L 2 = L 3 I ˙ L 3 C 1 Q 1 + L 1 I ˙ L 1 = L 2 I ˙ L 2
Taking Laplace transform on both sides of all equation leads to the following linear equations in the s-domain:
s Q 3 ( s ) − C 3 V C 3 = I C 3 ( s ) s Q 2 ( s ) − C 2 V C 2 = I C 2 ( s ) s Q 1 ( s ) − C 1 V C 1 = I C 1 ( s )
I C 3 ( s ) = I C 2 ( s ) + I L 3 ( s ) I C 1 ( s ) = I C 3 ( s ) + I L 1 ( s ) I C 2 ( s ) = I C 1 ( s ) + I L 2 ( s )
C 3 Q 3 ( s ) + s L 3 I L 3 ( s ) = s L 1 I L 1 ( s ) C 2 Q 2 ( s ) + s L 2 I L 2 ( s ) = s L 3 I L 3 ( s ) C 1 Q 1 ( s ) + s L 1 I L 1 ( s ) = s L 2 I L 2 ( s )
Plugging in all constants and solving for Q 1 ( s ) , Q 2 ( s ) and Q 3 ( s ) gives:
Q 1 ( s ) = 1 6 s 2 + 1 1 6 0 s Q 2 ( s ) = ( 1 1 s 2 + 1 ) ( 1 6 s 2 + 1 ) 4 s ( 6 1 6 s 2 + 3 1 ) Q 3 ( s ) = − ( 1 1 s 2 + 1 ) ( 1 6 s 2 + 1 ) 6 s ( 1 0 5 6 s 2 + 7 1 )
Using an online inverse Laplace transform calculator:
Q 1 ( t ) = 1 0 cos ( 4 t ) Q 2 ( t ) = 2 0 cos ( 1 1 1 1 t ) − 6 cos ( 4 t ) Q 3 ( t ) = − 6 cos ( 4 t ) − 3 0 cos ( 1 1 1 1 t )
The energy stored in the capacitors at any instant is:
E C ( t ) = 2 C 1 Q 1 2 + 2 C 2 Q 2 2 + 2 C 3 Q 3 2
At time t = 0 there is no current flowing through inductors, this means that the total energy of the system at that instant is stored in the capacitors. Therefore, the required answer is:
E C ( 0 ) E C ( 4 ) = 0 . 1 5