7 Cascaded Quantum Gates
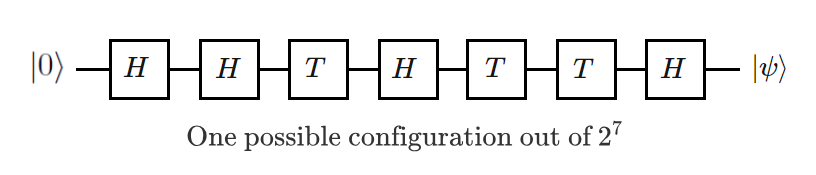
Suppose we feed a qubit with initial state into a system consisting of cascaded quantum logic gates. Only the quantum gates and are available to manipulate the qubit. The final state results from a sequence of operations:
The two available component gates are defined below:
The gate system can be configured in different ways. The probability of observing output in the state can take distinct values. If the arithmetic mean of these probability values is , enter .
Note: denotes the floor function .
Supplemental Information:
Inspiration
Prereq #1
Prereq #2
The answer is 546.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The following code evaluates all 128 possibilities. The process is the following:
1) For each binary permutation from 0 0 0 0 0 0 0 to 1 1 1 1 1 1 1 , assign the H matrix to 0 and the T matrix to 1
2) Multiply all 7 matrices together sequentially to yield an aggregate system matrix
3) Multiply the aggregate system matrix by ( 1 0 ) to yield a result in the form ( α β )
4) Calculate the probability of measuring the state ∣ 0 ⟩ = ( 1 0 ) by calculating ∣ α ∣ 2
5 ) Print analyses and results for all system configurations, and produce a sorted list of probabilities for measuring state ∣ 0 ⟩ = ( 1 0 )
Results (pastebin)
The probabilities for measuring the ∣ 0 ⟩ state can be the following:
0 . 0 0 0 0 0 0 0 0 0 . 1 4 6 4 4 6 6 1 0 . 5 0 0 0 0 0 0 0 0 . 5 7 3 2 2 3 3 0 0 . 7 5 0 0 0 0 0 0 0 . 8 5 3 5 5 3 3 9 1 . 0 0 0 0 0 0 0 0
Code: