(8) - Incoming and Outcoming
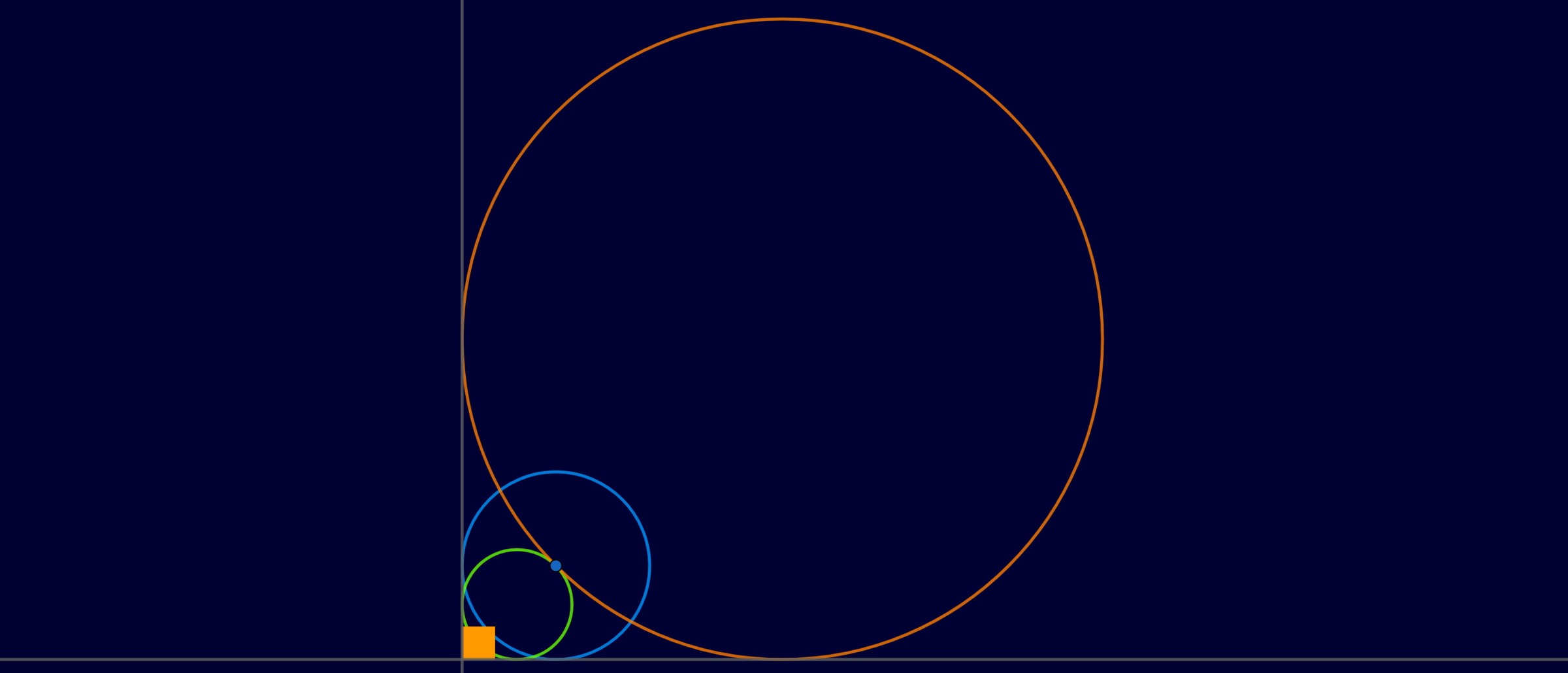 The orange circle and the green circle intersect at the center of the blue circle. If the radius of the orange, green and blue circle are respectively
m
,
n
and
p
. Calculate the value of
p
m
+
n
.
The orange circle and the green circle intersect at the center of the blue circle. If the radius of the orange, green and blue circle are respectively
m
,
n
and
p
. Calculate the value of
p
m
+
n
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I never thought of doing so. Thanks.
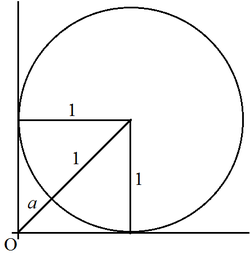 Consider a standard unit circle with its circumference tangent to the
x
-axis and
y
-axis. Let the shortest distance from the origin
O
to the circumference be
a
, then we note that
a
=
2
−
1
.
Consider a standard unit circle with its circumference tangent to the
x
-axis and
y
-axis. Let the shortest distance from the origin
O
to the circumference be
a
, then we note that
a
=
2
−
1
.
- For the orange circle with radius m , the corresponding distance a m = ( 2 − 1 ) m ⟹ m = 2 − 1 a m .
- And we note that a m = ( 2 + 2 − 1 ) n = ( 2 + 1 ) n ⟹ n = 2 + 1 a m .
- Similarly, a m = ( 1 + 2 − 1 ) p = 2 p ⟹ p = 2 a m .
Therefore, p m + n = 2 a m 2 − 1 a m + 2 + 1 a m = 2 1 2 + 1 + 2 − 1 = 2 2 × 2 = 4 .
That is a great solution! Thanks.
If we consider the two perpendicular lines as axes, the family of circles that are tangent to both have equations ( x − r ) 2 + ( y − r ) ² = r 2 (the parameter r corresponds to the circles' radii). Which of these pass through the point ( p , p ) (the centre of the blue circle)?
Plugging in, we have ( p − r ) 2 + ( p − r ) ² = r 2 , or r 2 − 4 p r + 2 p 2 = 0 .
This is a quadratic in r . The sum of the two solutions is 4 p (by Vieta).
But clearly the two solutions are m and n . So m + n = 4 p , and the answer is 4