8 Islands
Eight islands (orange circles) are connected to one another by bridges (blue lines), as shown in the diagram above.
If one island cannot be visited more than once, how many ways are there to go from island A to island B using these bridges?
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It gets easier if you first count all the ways in which you enter B from the left, then all the ways in which you enter from the bottom, and lastly all the ways in which you enter from the right.
Ways to enter from the left :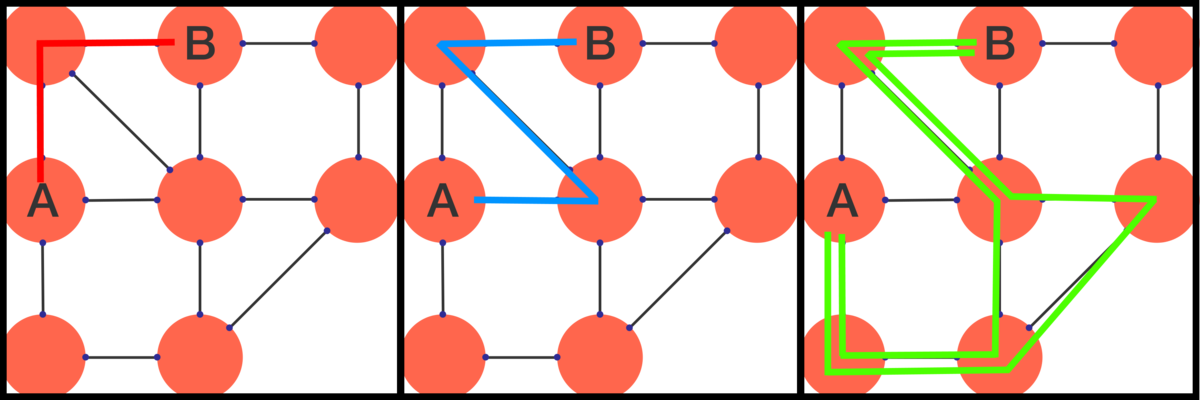
Ways to enter from below :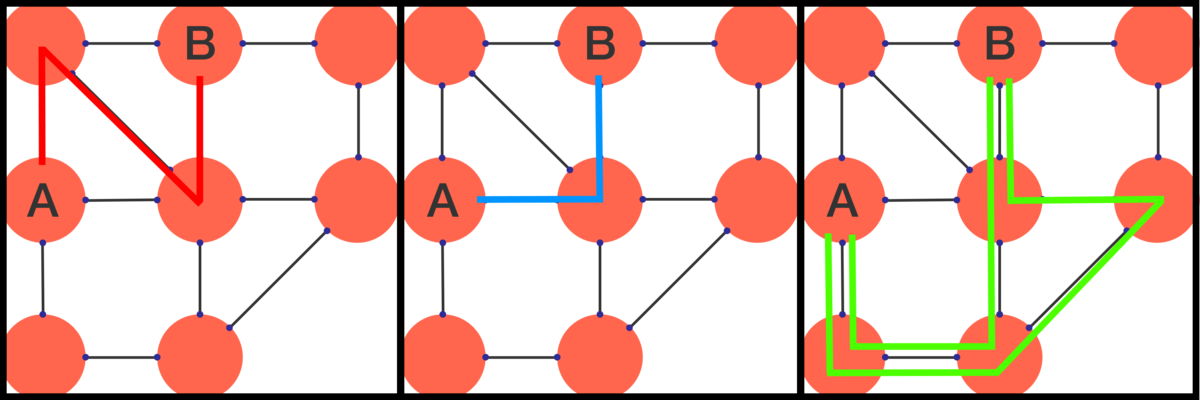
Ways to enter from the right :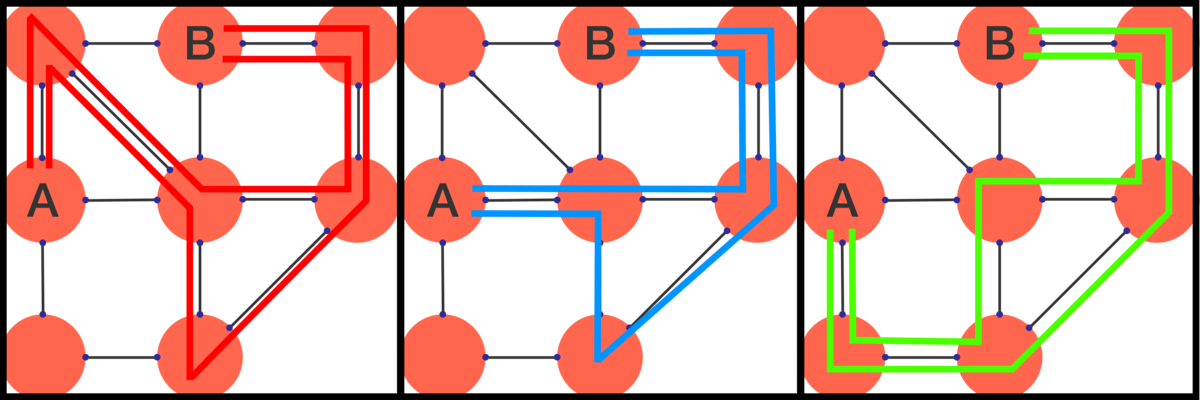
It becomes easier to see that these are all the possible ways to get from A to B (given that you can't enter an island twice) if you think about all the ways to reach B when exiting A from above (as shown in red), then all the ways if you exit to the right (as shown in blue) and finally all the ways if you exit from the bottom (as shown in green).
Finally you just add all the ways to enter B from the left, from below and from the right and end up with 4+4+6=14 total possible ways.