8 Operations
1 □ 2 □ 3 □ 4 □ 5 □ 6 □ 7 □ 8 □ 9 = 3 3
Seven of the eight " □ "s above are filled with " + ", and the other one with " − ".
Before which integer should the " − " sign be placed to make the equation true?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Do you think the phrasing is clear? There's a report that they counted the 5th box instead.
Log in to reply
My suggestion:
Seven of the eight " □ "s are filled with " + " and one with " − ". Before which integer should the " − " be placed to make the equation true?
All 9 digits when added makes 4 5 . One needs to swap sign to make it 3 3 , changing the outcome by 4 5 − 3 3 = 1 2 . This will happen with 1 2 / 2 = 6 .
Just wanted to make a de-algebra version, since this problem is solvable by students who haven't had algebra yet.
I did the same way.
To solve this problem, we are given that 7 of the 8 operation signs in this sequence are addition symbols, and one is a subtraction symbol. First, we must add all of these numbers, which yields the result of 4 5 . We then have to realize that 4 5 is 1 2 greater than the number value which we must obtain, which is 3 3 . Secondly, we can see that to get this result, we will have to subtract one of the integers from this sequence, which we will call y . If the value of the set of numbers added together, S is 4 5 , then this will be 4 5 − x . When we subtract x from the sequence however, we are subtracting the number twice, once from the original sequence, and then adding its negative value back into S . In this context, we are concerned with the magnitudes of the numbers, so we can see this through this:
∣ − x ∣ + x = x + x = 2 x
Since the value of all of the numbers deviates 1 2 units from the value of the hidden operations at a value of 3 3 , we can see that 2 x , which is deviation, is equal to 1 2 . Because of this x = 6 . Therefore, the number that we must place the subtraction sign before is 6 .
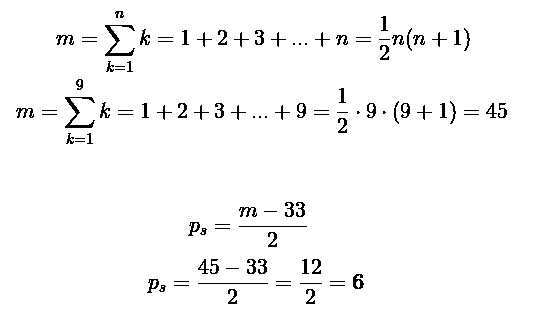
We need to put minus before 6.
Again, the sum (45)-2x=33 yields the solution.
Relevant wiki: Arithmetic Puzzles - Fill in the Blanks
We note that 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 4 5 . If we replace an integer k between 1 and 9 with 0, the sum of the 9 integers is 4 5 − k . If we now replace 0 with − k , the sum of the nine integers is 4 5 − 2 k . Therefore, 4 5 − 2 k = 3 3 , we have k = ( 4 5 − 3 3 ) / 2 = 6 .