829999 students did this problem wrong!
A tetrahedron is glued to a side face of the square pyramid whose edge lengths are all equal. How many faces does the new solid have?
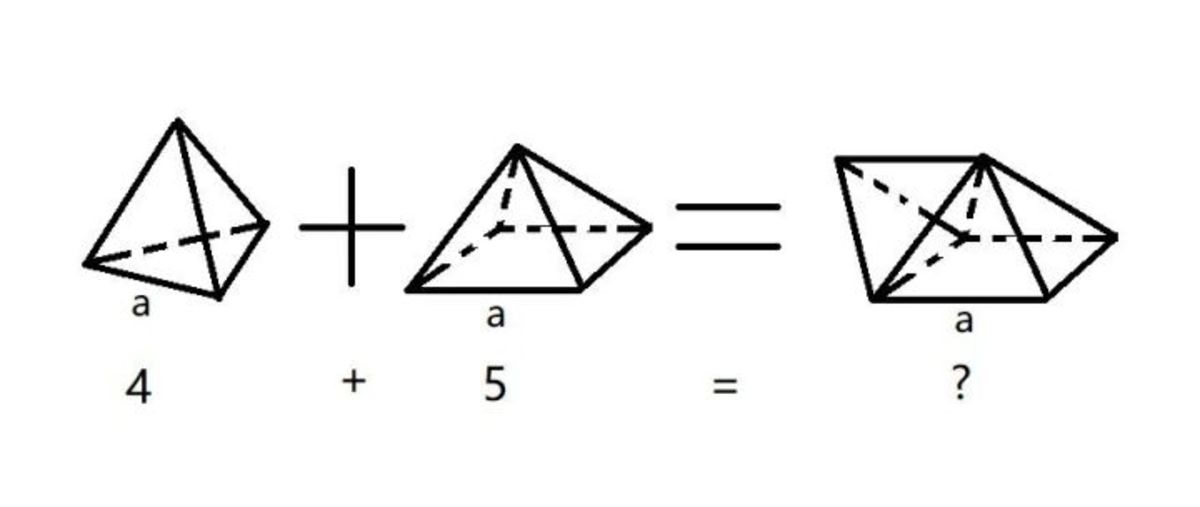
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Draw the red and blue triangles as follows:
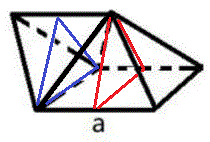
Both red and blue triangles have two side lengths of the height of the equilateral triangle face and one side length of the side of the equilateral triangle face, so they are congruent by SSS congruence. That means they can be used as base faces of a triangular prism, which means some of the side equilateral triangles are co-planar, so that the new solid has a total of 5 faces .
Maybe when seeing the answer you may have already known that, when combining them together, their side faces are coplaner, causing the further reduction of faces. But I think it interesting to show why it is the case:
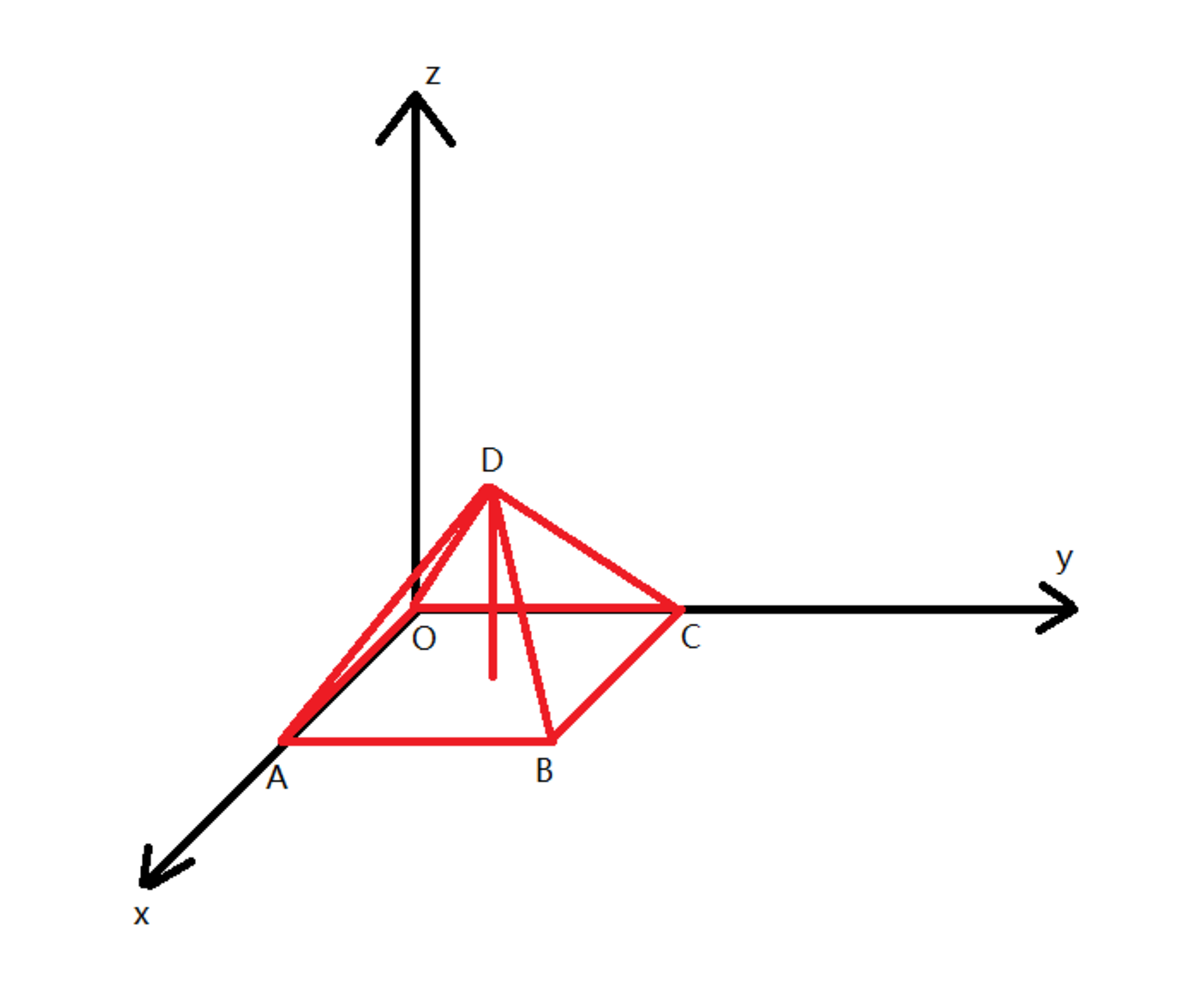
Let A ( 1 , 0 , 0 ) , B ( 1 , 1 , 0 ) , C ( 0 , 1 , 0 ) , then it's easy to show that D ( 2 1 , 2 1 , 2 2 ) , let's assume that the other point of the tetrahedron, E has the coordinate ( x , y , z ) .
Then we have:
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ ( x − 1 ) 2 + y 2 + z 2 = 1 x 2 + y 2 + z 2 = 1 ( x − 2 1 ) 2 + ( y − 2 1 ) 2 + ( z − 2 2 ) 2 = 1
Solving it gives us (negate z = − 6 2 ):
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ x = 2 1 y = − 2 1 z = 2 2
So E ( 2 1 , − 2 1 , 2 2 ) , and it's easy to show that B D ∥ A E , C D ∥ O E , B C ∥ O A , so plane B C D ∥ O A E .
Thus the resulting solid is actually a prism, so it has 5 faces.
https://www.youtube.com/watch?v=rXIzUtLG2jE