9 circle problem

Well,to solve this mysterious problem,let's first prove a lemma .

Lemma $\overline{PY_{1}}\cdot\overline{PY_{2}}=$ $P$ 's power of $\od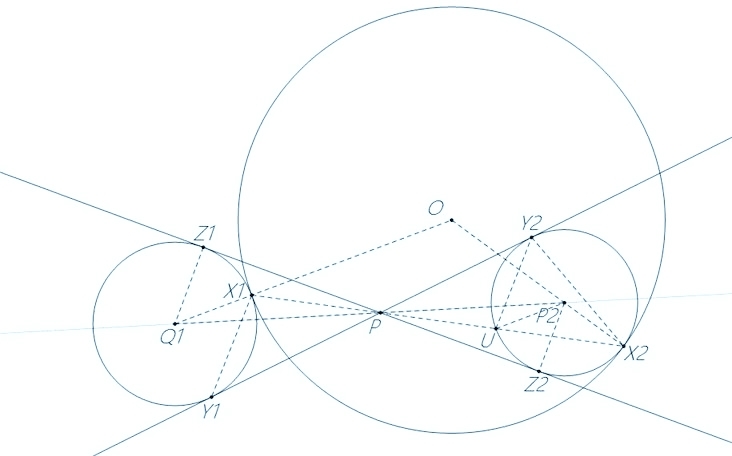ot O(<0)$ .

Proof First,let's show that $\overline{PX_{1}}\cdot\overline{PX_{2}}=$ $P$ 's power of $\odot O$ .It's equivalent to show $X_{1},P,X_{2}$ are collinear.Note that $Q_{1}Z_{1}\perp Z_{1}Z_{2}$ and $P_{2}Z_{2} \perp Z_{1}Z_{2}$ give us $Q_{1}Z_{1}//P_{2}Z_{2}$ $\Longrightarrow$ $\frac{Q_{1}Z_{1}}{P_{2}Z_{2}}=\frac{PQ_{1}}{PP_{2}}$ $\Longrightarrow$ $\frac{Q_{1}X_{1}}{P_{2}X_{2}}=\frac{PQ_{1}}{PP_{2}}$ $\Longrightarrow$ $\frac{Q_{1}X_{1}}{X_{1}O}\cdot\frac{OX_{2}}{X_{2}P_{2}}\cdot\frac{P_{2}P}{PQ_{1}}=1$ .Hence by Menelaus's Theorem,we have $X_{1},P,X_{2}$ are collinear.

Now let $U$ denotes the the second intersection of the line $X_{1}PX_{2}$ and $\odot P_{2}$ . A homothetic transformation whose centre and ratio are $P$ and $-\frac{R_{\odot P_{2}}}{R_{\odot Q_{1}}}$ respectively helps us throw $Y_{1}$ , $X_{1}$ to $Y_{2}$ , $U$ ,respectively.Thus, $Y_{1}X_{1}//Y_{2}U$ $\Longrightarrow$ $\angle X_{1}Y_{1}P=\angle UY_{2}P=\angle Y_{2}X_{2}U=\angle Y_{2}X_{2}P$ $\Longrightarrow$ $X_{1},Y_{1},X_{2},Y_{2}$ are concyclic $\Longrightarrow$ $\overline{PY_{1}}\cdot\overline{PY_{2}}=\overline{PX_{1}}\cdot\overline{PX_{2}}=$ $P$ 's power of $\odot O$ . $\Box$

Come back

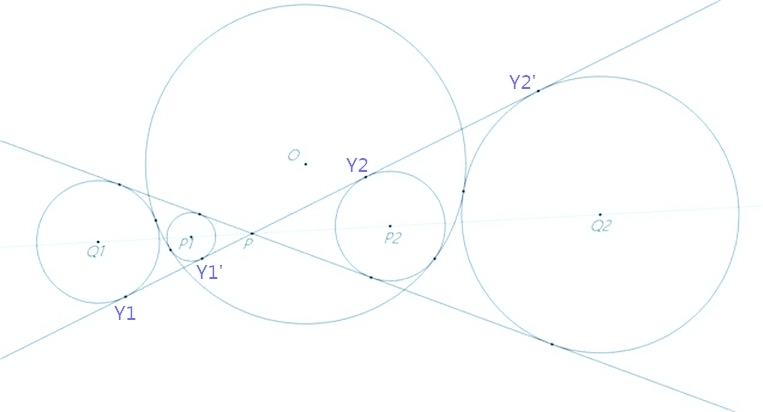
Using the lamma,we have $\overline{PY_{1}}\cdot\overline{PY_{2}}=\overline{PY_{1}'}\cdot\overline{PY_{2}'}=$ $P$ 's power of $\odot O$ $\Longrightarrow$ $\frac{PY_{1}'}{PY_{1}}=\frac{PY_{2}}{PY_{2}'}$ $\Longrightarrow$ $\frac{R_{\odot{P_{1}}}}{R_{\odot{Q_{1}}}}=\frac{R_{\odot{P_{2}}}}{R_{\odot{Q_{2}}}}$ . So $r_{2}=r_{4}\cdot \frac{r_{6}}{r_{8}}=\boxed{12}$

About the Appendix

$r_{3}r_{4}r_{5}r_{6}=(R^{2}-d^{2})^{2}$ (easy to get from our lemma,as you can express $r_{3}r_{5}$ and $r_{4}r_{6}$ as $tan^{2}\theta\cdot (R^{2}-d^{2})$ and $cot^{2}\theta\cdot (R^{2}-d^{2})$ respectively,here $\theta$ is a half of the acute angle that formed by $l$ and $m$ in the picture.)