90 degree angle in clock.

Geometry Level pending

How many times does the minute hand and hour hand of an analog clock form a 90 degree angle in 12 hours?
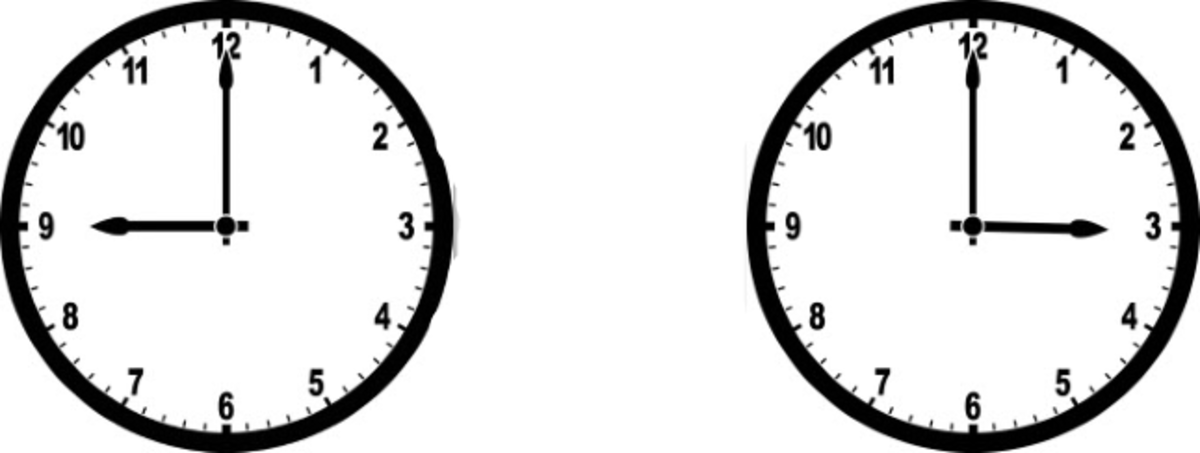
Note: its a standard 12 division clock as below. Example:

11 22 23 24 12

1 solution

Saad Khondoker
Jan 31, 2021

Observation:
In every hour 90 degree is formed twice except for between 2 to 3 o'clock and 8 to 9 o'clock where it is formed only once. So the answer is 12 * 2 - 2 = 22.

Mathematical approach:
At 3:00 we see a 90 degree. Lets assume after x minutes we will see another 90 degree with same orientation (from the same side). In 1 minute the minute hand moves x * 360/60 = 6x degree. In 1 minute the hour hand moves x * 360/(12*60) = x/2 degree. The minute hand will rotate 360 degree more than the hour hand. So we get,
6x = x/2 + 360
=> x = 2 * 360/11
so in 12 hours, we see it [12 * 60 / (2 * 360/11)] times = 11 times.
Similarly, at 9:00 we see a 90 degree but in different orientation. Doing the same calculation, we get another 11.
So total number of times 90 degree is formed is 11 + 11 = 22 times.

I made a computational error... so I'm writing this here.

Let the total angle the minute hand rotates through w.r.t a line connecting the center of the clock to the 12 be $\theta$ . Let the angle the hour hand rotates through be $\beta$

It follows that:

$\beta ( \theta ) = \frac{30}{360} \theta \quad \text{Eq1}$

A right angle can be formed of two types, $\theta$ leads $\beta$ by $90 ^\circ$ or $270 ^\circ$ as shown in the image.

We are looking for the number of solutions to:

$\theta - \beta = ( 2n-1 ) 90 \quad \text{Eq2}$

where $n \in \mathbb{N}$

Subbing Eq1 $\to$ Eq2 for $\beta$ we find:

$\theta = \frac{( 2n-1 ) 90}{ 1 - \frac{30}{360} } \quad \text{Eq3}$

after 12 hrs:

$\theta = 12 \cdot 360 ^\circ = 4320 ^\circ \quad \text{Eq4}$

Sub Eq4 $\to$ Eq3 and solve for $n$

$n = \lfloor 22.5 \rfloor = 22$

Thanks for the problem!

Eric Roberts - 4 months, 1 week ago

90 degree angle in clock.

1 solution

0 pending reports