90vertigo
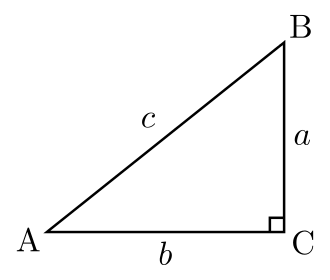 If the side length of
is
, and
and
are positive integers, find the value of
.
If the side length of
is
, and
and
are positive integers, find the value of
.
The answer is 134854567850.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
See that a 2 = c 2 − b 2 .
∴ 8 5 7 2 = ( c + b ) ( c − b )
But as b , c are positive integers, none of them is zero, and 8 5 7 is a prime number.
Hence the only way in which we can factorize the number 8 5 7 2 into two different integer factors, is 8 5 7 2 × 1
∴ c + b = 8 5 7 2 = 7 3 4 4 4 9 , c − b = 1
∴ b = 3 6 7 2 2 4 , c = 3 6 7 2 2 5
Required answer is 2 c + b c = c ( 2 + b ) = 3 6 7 2 2 5 × 3 6 7 2 2 6 = 1 3 4 8 5 4 5 6 7 8 5 0