Area Of An Innocent Right Triangle

It can be shown using AM-GM that the altitude to the hypotenuse is at most half of the hypotenuse. It follows that there is no such triangle, and hence the correct answer is $\boxed{\text{This question is flawed}}$ .

Source: A post on MSE

To quote @Calvin Lin,

...This is one reason why I stress considering the possibility of the geometrical setup and ensuring that it actually exists.

The main point of checking the existence of the possibility of a geometric structure isn't necessarily that the question is deliberately trying to fool you (like this one), but that checking why a geometric structure exists will give you a pointer towards some narrow but definite parts of a diagram that have more restrictions imposed on them (otherwise the diagram would cease to exist). These parts of a diagram should theoretically be easier to investigate due to having more restrictions on them. This is still true in olympiad maths, not just pre-olympiads.

If the area of triangle is 160.Then it means if a,b are legs of the triangle then $\frac{ab}{2}=160$ it follows that ab=320 and 2ab=640 and $a^2+b^2$ =400 (Pythagoras theorem).Subtracting 1st equation from 2nd we get $a^2+b^2-2ab$ =-240 as $a^2+b^2-2ab$ is a square of (a-b) and square of anything cant be negative.It isnt possible.

From the diagram above, we get:

$AB = \sqrt{16^{2}+x^{2}}$ and $BC = \sqrt{16^{2}+(20-x)^{2}}$ .

Then, combining them and simplifying, we have $x^{2}-20x+206=0$ , which has no real solutions.

Consider the right angled triangle with its hypotenuse as the diameter of a circle. Clearly the altitude cannot be more than the radius of circle. The radius of circle is half of hypotenuse 10.

The possible setup for right triangle with hypotenuse of 20: 12 and 16. If the hypotenuse was reduced into 16, then the setup would be impossible as there are two sides with 16 of length. Therefore the triangle should not be right anymore, but it will become isosceles one.

Circumscribe the triangle into a circle or radius 20 and acording to the figure $x+y = 20$ by $MA-MG$ we see that $20=x+y \geq 2\sqrt{xy} \Rightarrow 10 \geq \sqrt{xy}$ Therefore there is not a triangle with this measures.

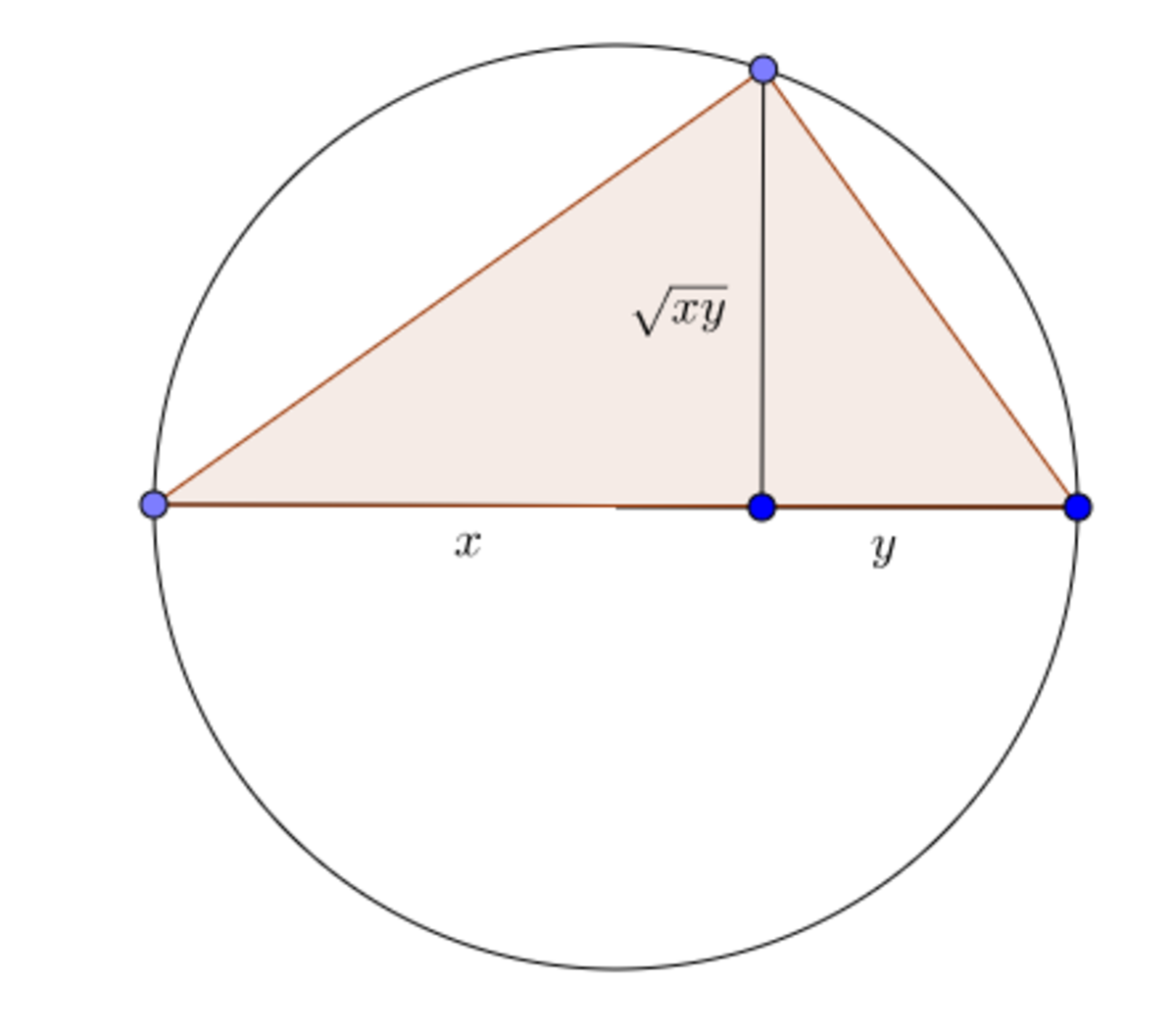
In any right triangle, the altitude divides the hypotenuse in two parts, with respective lengths x and y, satisfying:

x + y = length of hypotenuse

x * y = (length of altitude)²

In this problem:

x + y = 20

x * y = 16² = 256

This system of equations has no real solution (the graphs of each equation don't touch each other).

Therefore, this right triangle is not possible.