A 23x23 square 1.0

It is possible to cover the $23\times 23$ square with only one $1\times 1$ s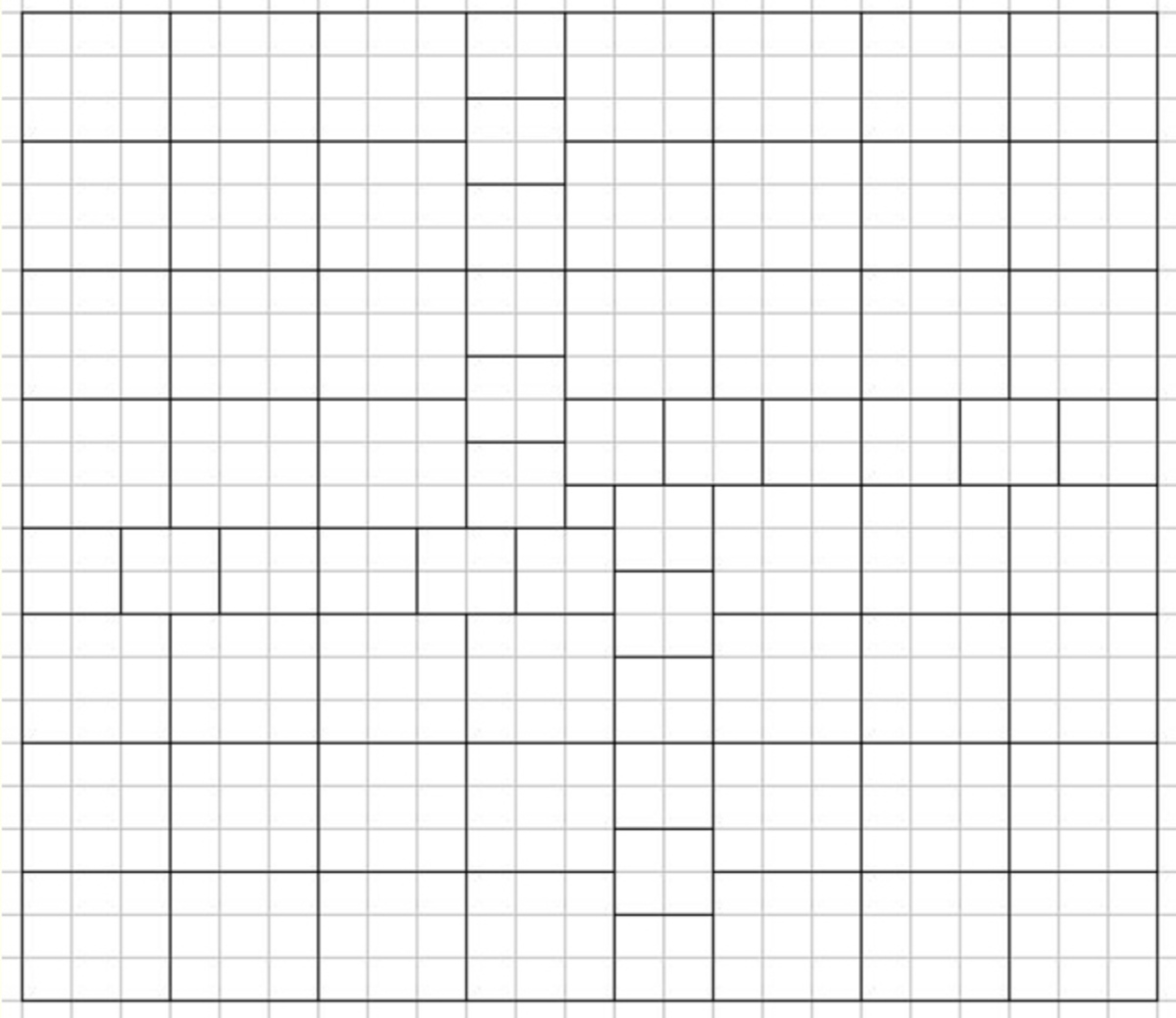quare. But is this the minimum? We will prove that 1 is the minimum!

Suppose that we covered the $23\times 23$ square with only $2\times 2$ and $3\times 3$ squares. If we colour the $1.,\space 4.,\space 7., \space 10.,\space 13.,\space 16.,\space 19.,\space 22.$ rows black, then there are $8*23$ black, and $15*23$ white cells. Every $2\times 2$ square covers $4$ or $2$ white cells, and every $3\times 3$ square covers exactly 6 white cells. So every square covers an even number of white cells, but $15*23$ is odd.

So the minimum of $1\times 1$ squares is $\boxed{1}$ .