A 24 Cornered Cube!

A corner is a part of two plains of the original cube plus a triangular small plain. Two big original plain has eight corners so there will be 2 * 7 =14 surface diagonals out of which one where they meet is common to both. So
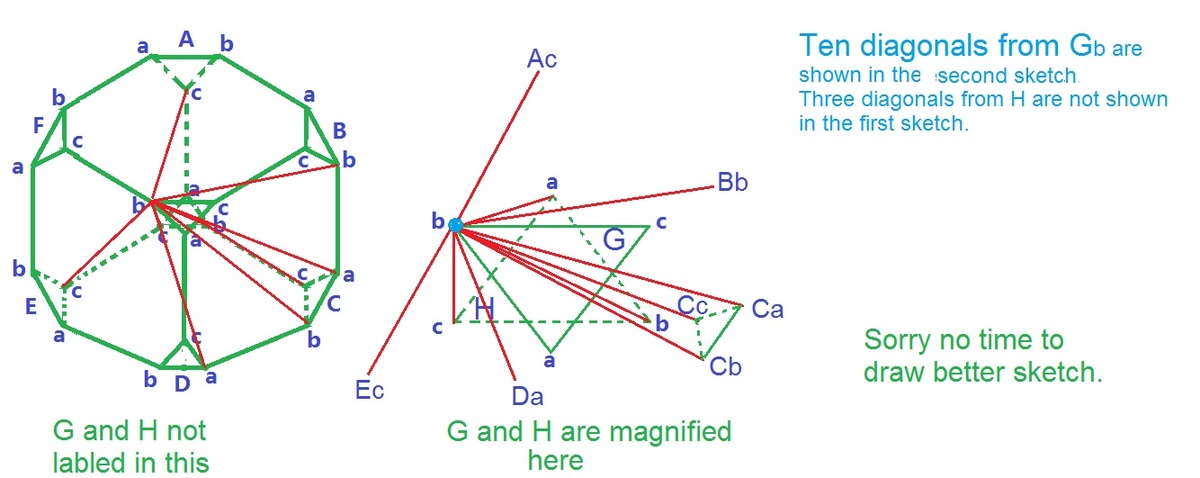
there are 13 suface diagonals. The diagonals of the triangular small plain are included in the big plains. Total diagonals from each corner are 24-1=23. So non surface diagonals from a corner are 23-13=10. There are 24 corners. So we counted 10 * 24=240. But a diagonal was counted from both the corners in two opposite directions. Diagonal is directionless. So 240/2= 120 diagonals are through the solid.

Or. Take the corner Gb. The sketch shows all 10 diagonals from Gb.

Each vertex can connect with 23 others, giving 23 'diagonals'. Now let us eliminate those which lie of an edge or a face (hence not 'inside' the solid)

Each vertex is a part of two octagonal faces*. There are 7 other vertices in each face. So out of the 23 vertices, 7 x 2 = 14 vertices give 'diagonals' lying on the face. One of these diagonals will be the edge where the two faces meet, which will be counted twice. So only 23 - 13 = 10 diagonals will go through the body.

Count these for all 24 vertices, giving 240 'inner diagonals' but each is counted twice as connecting vertex A to B and then again connecting vertex B to A, yielding 240/2 = $\textbf {120}$

• Triangular faces need not be considered, as they only give 'diagonals' which are edges already a part of the octagonal faces.