A , B , C , D go for a walk
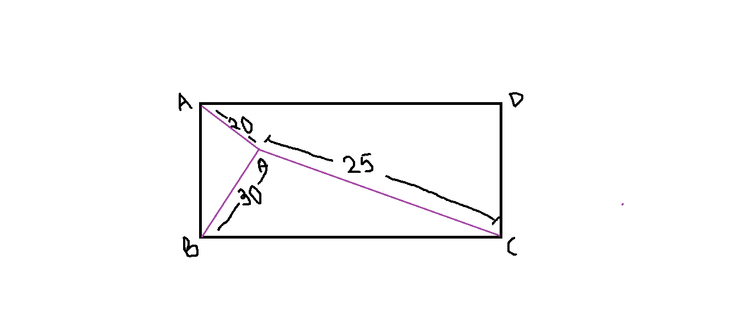A , B, C , D walk towards a point P taking the shortest path from the four vertices of a rectangle . After they reach the point P, which is inside the rectangle , it is found that the distance traveled by A is 20m , B is 30m , C is 25m (as shown in the "cool" figure).Find the distance traveled by D.
FIGURE NOT TO SCALE
HAVE FUN!!!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Construction: Join DP and draw a line XPY parallel to AB passing through P. Now, AXYB and DXYC are rectangles.
So, AX=BY and DX=CY.
In right triangle AXP, AP^2 = AX^2 + XP^2 (By Pythagoras Theorem) ------(1)
In right triangle CYP, CP^2 = CY^2 + YP^2 (By Pythagoras Theorem) ------(2)
Adding (1) and (2),
AP^2 + CP^2 = AX^2 + XP^2 + CY^2 + YP^2
AP^2 + CP^2 = BY^2 + XP^2 + DX^2 + YP^2 (Because AX=BY and DX=CY.)
AP^2 + CP^2 = (BY^2 + YP^2) + (XP^2 + DX^2)
AP^2 + CP^2 = BP^2 + DP^2 -----------(3)
Now, AP = 20 m, BP = 30 m and CP = 25 m
Put these values in relation(3) to get DP = 5 root5 m