A beautiful circuit

Electricity and Magnetism Level 5

Consider the following circuit which consists of 3 3 current sources, 16 16 resistors arranged in an octagon, and a load in parallel with a resistor.

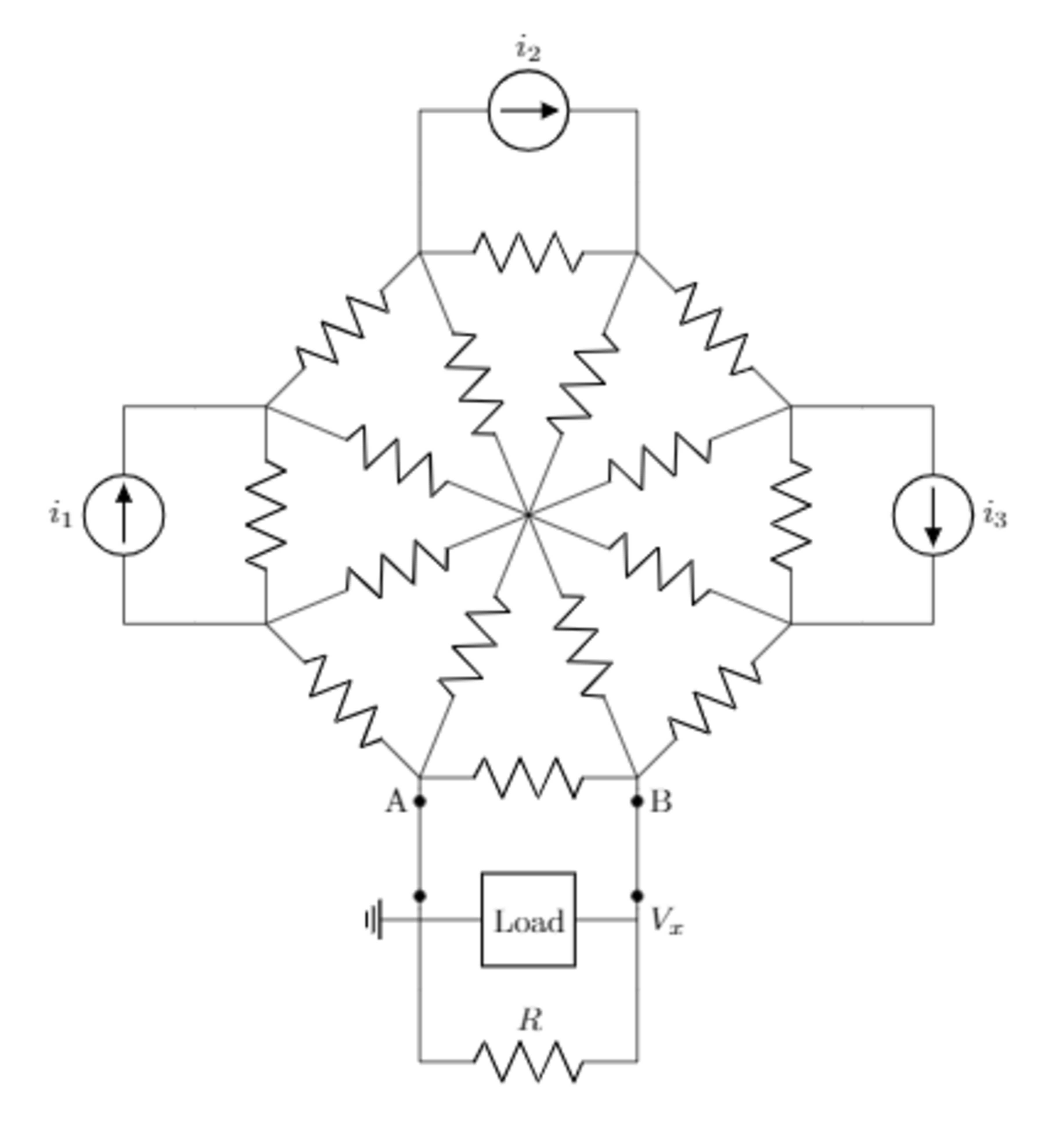
Furthermore, consider three different versions of this circuit which have three different loads.

  • A resistor of resistance R L = 1 k Ω R_L = 1\rm k\Omega . Determine V 1 = V x V_1 = V_x .
  • A capacitor of capacitance C C . Determine V 2 = V x ( τ ) V_2 = V_x(\tau) , the voltage V x ( t ) V_x(t) after a single time constant, if switches A and B are opened at t = 0 t = 0 .
  • An inductor of inductance L L . If the switches are opened at t = 0 t = 0 , determine V 3 = V x ( τ ) V_3 = V_x(\tau) .

Calculate V 1 + V 2 + V 3 V_1 + V_2 + V_3 (in volts) to 1 decimal place.

Details and assumptions:

  • All of the resistors are of identical resistance R = 50 Ω R = 50\rm \Omega .
  • i 1 = 1 A i_1 = 1 \rm A , i 2 = 2 A i_2 = 2\rm A , i 3 = 3 A i_3 = 3\rm A .
  • Assume that switches A and B have been closed for a very long time so the circuit is in steady state prior to the opening of the switches.

This question is inspired by this problem .


The answer is 23.4.

Charley Shi by Charley Shi , 19, New Zealand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Charley Shi
Apr 7, 2021

My solution.

2 Helpful 2 Interesting 2 Brilliant 0 Confused
Steven Chase
Apr 7, 2021

Fun problem. My solution has a lot in common with the problem author's so I will just show how to solve for the Thevenin equivalent of the top portion without using superposition.

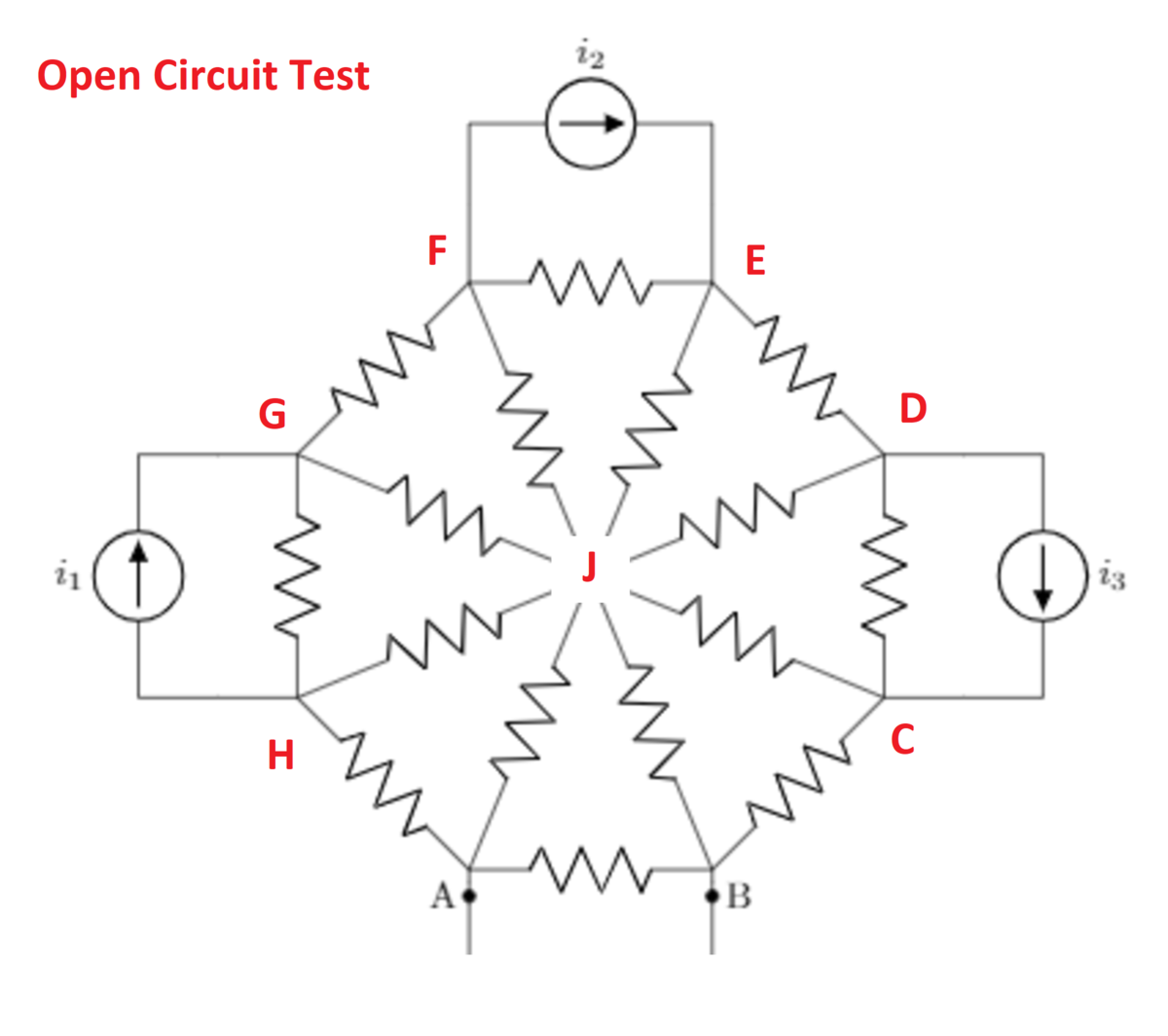
First calculate the open circuit voltage between A and B. I labeled the node voltages ( A , B , C , D , E , F , G , H , J ) (A,B,C,D,E,F,G,H,J) . The sum of the currents out of each node should be zero. I used a hill climbing algorithm to search for all nine node voltages such that this condition is satisfied. Then the Thevenin internal voltage is the voltage at B B minus the voltage at A A with the terminals open. Results are printed at the end of the first piece of code.

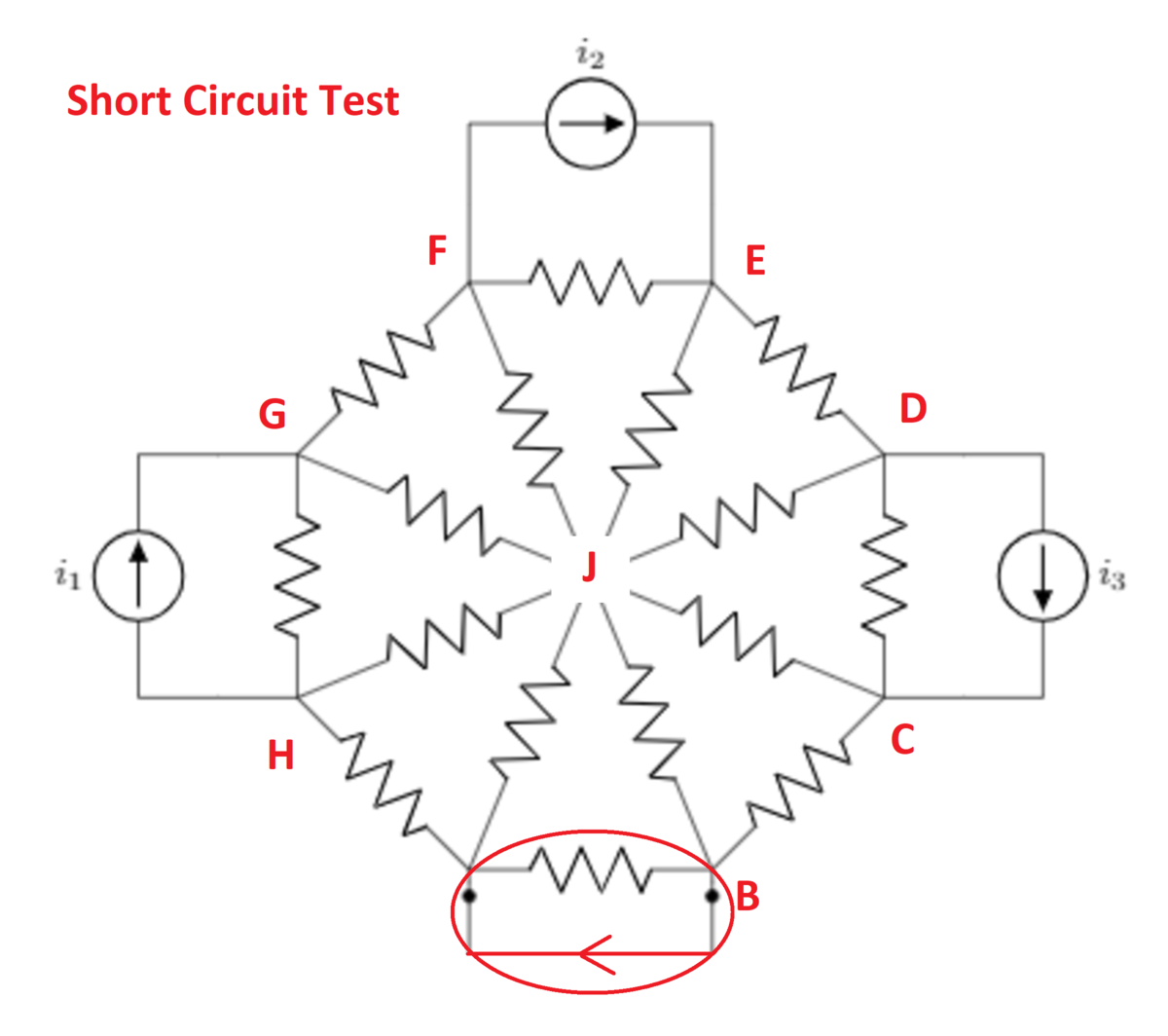
Then calculate the short circuit current. In this case, node B becomes a "supernode", and we again search for the node voltages such that the sum of currents out of each node is zero. The short circuit current is the current into one end of the supernode (consisting of two currents flowing in on paths JB and CB). The results are printed at the end of the second piece of code. The Thevenin resistance is the open circuit voltage divided by the short circuit current. 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
 
# Open Circuit Solution

import math
import random

R = 50.0

I1 = 1.0
I2 = 2.0
I3 = 3.0

A = 50.0 * random.random()
B = 50.0 * random.random()
C = 50.0 * random.random()
D = 50.0 * random.random()
E = 50.0 * random.random()
F = 50.0 * random.random()
G = 50.0 * random.random()
H = 50.0 * random.random()
J = 50.0 * random.random()


delta = 0.001

minres = 99999999.0

########################################################################################

for j in range(0,2*10**6):

    Am = A + delta * (-1.0 + 2.0 * random.random())
    Bm = B + delta * (-1.0 + 2.0 * random.random())
    Cm = C + delta * (-1.0 + 2.0 * random.random())
    Dm = D + delta * (-1.0 + 2.0 * random.random())
    Em = E + delta * (-1.0 + 2.0 * random.random())
    Fm = F + delta * (-1.0 + 2.0 * random.random())
    Gm = G + delta * (-1.0 + 2.0 * random.random())
    Hm = H + delta * (-1.0 + 2.0 * random.random())
    Jm = J + delta * (-1.0 + 2.0 * random.random())

    IA = (Am - Hm)/R + (Am - Jm)/R + (Am - Bm)/R
    IH = (Hm - Am)/R + (Hm - Jm)/R + (Hm - Gm)/R + I1
    IG = (Gm - Hm)/R + (Gm - Jm)/R + (Gm - Fm)/R - I1
    IF = (Fm - Gm)/R + (Fm - Jm)/R + (Fm - Em)/R + I2
    IE = (Em - Fm)/R + (Em - Jm)/R + (Em - Dm)/R - I2
    ID = (Dm - Em)/R + (Dm - Jm)/R + (Dm - Cm)/R + I3
    IC = (Cm - Dm)/R + (Cm - Jm)/R + (Cm - Bm)/R - I3
    IB = (Bm - Cm)/R + (Bm - Jm)/R + (Bm - Am)/R
    IJ = (Jm-Am)/R+(Jm-Bm)/R+(Jm-Cm)/R+(Jm-Dm)/R+(Jm-Em)/R+(Jm-Fm)/R+(Jm-Gm)/R+(Jm-Hm)/R  

    res = math.fabs(IA)+math.fabs(IB)+math.fabs(IC)+math.fabs(ID)
    res = res + math.fabs(IE)+math.fabs(IF)+math.fabs(IG)+math.fabs(IH)+math.fabs(IJ)

    if res < minres:

        minres = res

        A = Am 
        B = Bm 
        C = Cm 
        D = Dm 
        E = Em 
        F = Fm 
        G = Gm 
        H = Hm 
        J = Jm 

########################################################################################

print minres
print ""
print A
print B
print C
print D
print E
print F
print G
print H
print J
print ""
print (B - A)

print ""
print "###########################"
print ""

#>>> 
#3.97835538863e-05

#22.2817172997
#37.5196475746
#67.5196910467
#-7.71820787106
#36.5676060087
#-5.33722772032
#24.6627582421
#6.56757676416
#22.7579936468

#15.2379302749

###########################

#>>> 


  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
 
# Short Circuit solution

import math
import random

R = 50.0

I1 = 1.0
I2 = 2.0
I3 = 3.0

B = 50.0 * random.random()
C = 50.0 * random.random()
D = 50.0 * random.random()
E = 50.0 * random.random()
F = 50.0 * random.random()
G = 50.0 * random.random()
H = 50.0 * random.random()
J = 50.0 * random.random()


delta = 0.001

minres = 99999999.0

########################################################################################

for j in range(0,2*10**6):

    Bm = B + delta * (-1.0 + 2.0 * random.random())
    Cm = C + delta * (-1.0 + 2.0 * random.random())
    Dm = D + delta * (-1.0 + 2.0 * random.random())
    Em = E + delta * (-1.0 + 2.0 * random.random())
    Fm = F + delta * (-1.0 + 2.0 * random.random())
    Gm = G + delta * (-1.0 + 2.0 * random.random())
    Hm = H + delta * (-1.0 + 2.0 * random.random())
    Jm = J + delta * (-1.0 + 2.0 * random.random())

    IH = (Hm - Bm)/R + (Hm - Jm)/R + (Hm - Gm)/R + I1
    IG = (Gm - Hm)/R + (Gm - Jm)/R + (Gm - Fm)/R - I1
    IF = (Fm - Gm)/R + (Fm - Jm)/R + (Fm - Em)/R + I2
    IE = (Em - Fm)/R + (Em - Jm)/R + (Em - Dm)/R - I2
    ID = (Dm - Em)/R + (Dm - Jm)/R + (Dm - Cm)/R + I3
    IC = (Cm - Dm)/R + (Cm - Jm)/R + (Cm - Bm)/R - I3
    IB = (Bm - Cm)/R + (Bm - Jm)/R + (Bm - Jm)/R + (Bm - Hm)/R
    IJ = (Jm-Bm)/R+(Jm-Bm)/R+(Jm-Cm)/R+(Jm-Dm)/R+(Jm-Em)/R+(Jm-Fm)/R+(Jm-Gm)/R+(Jm-Hm)/R  

    res = math.fabs(IB)+math.fabs(IC)+math.fabs(ID)
    res = res + math.fabs(IE)+math.fabs(IF)+math.fabs(IG)+math.fabs(IH)+math.fabs(IJ)

    if res < minres:

        minres = res

        B = Bm 
        C = Cm 
        D = Dm 
        E = Em 
        F = Fm 
        G = Gm 
        H = Hm 
        J = Jm 

########################################################################################

print minres
print ""
print B
print C
print D
print E
print F
print G
print H
print J
print ""
ISC = (C-B)/R + (J-B)/R

print ISC

print ""
print "###########################"
print ""

#>>> 
#2.94606486618e-05

#42.1176249152
#76.8466547636
#3.44762602221
#48.5216660647
#7.14221456346
#37.930351131
#21.6742293952
#34.9747910353

#0.551723919369

###########################

#>>>

1 Helpful 1 Interesting 1 Brilliant 0 Confused
Carsten Meyer
Apr 23, 2021

Here's a solution using symmetry and superposition to greatly simplify the network into only three loops. Before we begin, we normalize all currents, voltages, time and elements by the values given below: voltages: 1 V , currents: 1 A , time: 1 s ⇒ R : 1 Ω , C : 1 F , L : 1 H \begin{aligned} \text{voltages:}&&&\SI{1}{V}, &&&\text{currents:}&&&\SI{1}{A},&&&\text{time:}&&&\SI{1}{s}&&& \Rightarrow &&&&R:&&&\SI{1}{\ohm}, &&& C:&&&\SI{1}{F}, &&&L:&&&\SI{1}{H} \end{aligned} The network equations remain the same in the process, but now all currents, voltages, time and elements represent their normalized dimensionless counterparts.

Before switching ( t < 0 ) t<0)

The network is supposed to be in steady state for all three loads. First, the load is R L = 1 0 3 R_L=10^3 . In case of C C the load simplifies to an open circuit or equivalently R L → ∞ R_L\rightarrow\infty . In case of L L the load simplifies to a short circuit or equivalently R L = 0 R_L=0 . Let's keep R L R_L as a variable and solve all three cases together!

First we rewrite the current sources I 1 , 3 I_{1,3} into ( I 1 I 3 ) = ( 1 3 ) = ( 2 2 ) + ( − 1 1 ) = : I ⃗ c + I ⃗ d \begin{pmatrix} I_1\\I_3 \end{pmatrix}= \begin{pmatrix} 1\\3 \end{pmatrix}= \begin{pmatrix} 2\\2 \end{pmatrix} + \begin{pmatrix} -1\\1 \end{pmatrix} =:\vec{I}_c + \vec{I}_d Now we use superposition: First we only consider I ⃗ d \vec{I}_d , afterwards the remaining sources I ⃗ c , I 2 \vec{I}_c,\:I_2 together. In both cases, the entire network is symmetric - that was the reason to rewrite I 1 , 3 I_{1,3} in the first place!

When I ⃗ d \vec{I}_d is active, we flip the left current source to eliminate the sign: Voltages on the left and right have to be equal by symmetry! This leads to V x = 0 V_x=0 , so we can ignore this case.

In the other case, voltages on the left and right have to be negative equal by symmetry! Therefore, the entire middle axis of the network has to have the same potential as the middle node: We may connect the entire middle axis to the middle node without changing any voltages/currents! To do that, we need to split R L R_L and three resistances R R in half.

As voltages on the left and right are negative equal, we only need to consider the right half of the simplified network to calculate V x V_x . After merging parallel resistances at the top into R t R_t and parallel resistances at the bottom into R b R_b , we only have three loops left: 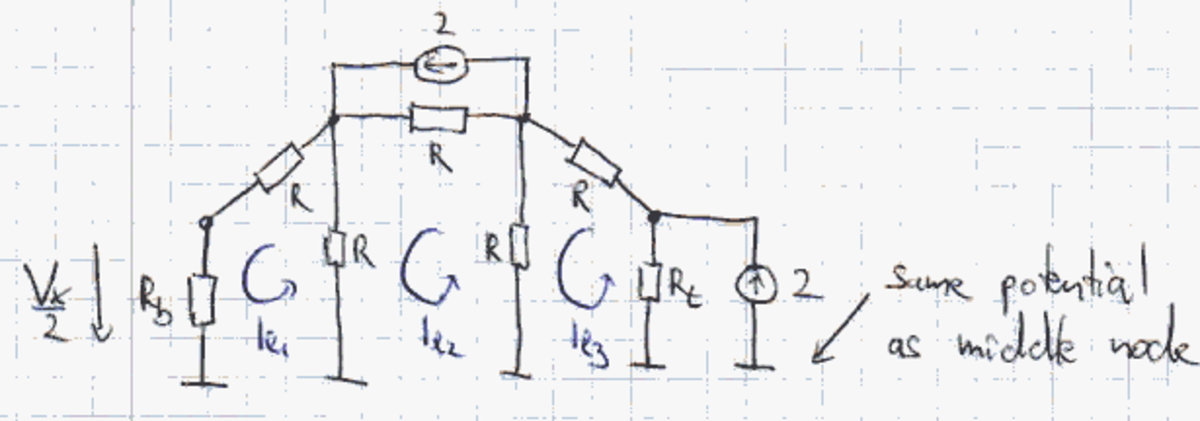Right half of the simplified network with loop currents (blue) Right half of the simplified network with loop currents (blue)

The top and bottom resistances are R t = R ∥ R 2 = R 3 , R b = R L 2 ∥ R 2 ∥ R 2 ∥ R = 1 2 R L + 5 R = R R L 2 R + 5 R L = : α ( R L ) R R_t=R\|\frac{R}{2}=\frac{R}{3},\qquad R_b=\frac{R_L}{2}\|\frac{R}{2}\|\frac{R}{2}\|R=\frac{1}{\frac{2}{R _L} + \frac{5}{R}}=\frac{RR_L}{2R+5R_L}=:\alpha(R_L)R

We rewrite the current sources and their parallel resistances into equivalent voltage sources to solve the resulting network by loop analysis: R ( 2 + α ( R L ) − 1 0 − 1 3 − 1 0 − 1 2 + 1 3 ) ( I l 1 I l 2 I l 3 ) = 2 R ( 0 1 1 3 ) R\begin{pmatrix} 2+\alpha(R_L) & -1 & 0\\ -1 & 3 & -1\\ 0 & -1 & 2+\frac{1}{3} \end{pmatrix}\begin{pmatrix} I_{l1}\\I_{l2}\\I_{l3} \end{pmatrix}=2R\begin{pmatrix} 0\\1\\\frac{1}{3} \end{pmatrix} We only need to solve for I l 1 I_{l1} , so we use Cramer's Determinant Rule: I l 1 = 2 ⋅ ( 2 + 1 3 ) + 1 3 7 ( 2 + α ( R L ) ) − ( 2 + α ( R L ) ) − ( 2 + 1 3 ) = 16 29 + 18 α ( R L ) = : f 1 ( R L ) , V x = 2 R b I l 1 = 2 R α ( R L ) I l 1 = 1600 α ( R L ) 29 + 18 α ( R L ) = : f 2 ( R L ) \begin{aligned} I_{l1}&=2\cdot\frac{ \left(2+\frac{1}{3}\right)+\frac{1}{3} }{ 7(2+\alpha(R_L)) - (2+\alpha(R_L)) - \left(2+\frac{1}{3}\right) }=\frac{16}{29+18\alpha(R_L)}=:f_1(R_L), &&&V_x&=2R_b I_{l1}=2R\alpha(R_L)I_{l1}=\frac{1600\alpha(R_L)}{29+18\alpha(R_L)}=:f_2(R_L) \end{aligned} Now we can finally compute the initial conditions for all three loads: R L = 1 0 3 : V x ( 0 − ) = f 2 ( 1 0 3 ) = 16000 1659 = V 1 , C : V x ( 0 − ) = lim ⁡ R L → ∞ f 2 ( R L ) = 1600 163 , L : I l 1 ( 0 − ) = f 1 ( 0 ) = 16 29 \begin{aligned} R_L=10^3:&& V_x(0^-)&=f_2(10^3)=\frac{16000}{1659}=V_1, &&&&& C:&& V_x(0^-)&=\lim_{R_L\rightarrow\infty}f_2(R_L)=\frac{1600}{163},&&&&& L:&& I_{l1}(0^-)&=f_1(0)=\frac{16}{29} \end{aligned}

After switching ( t ≥ 0 t\geq 0 )

We only need to consider the loads C , L C,\:L for which we have to compute V x ( τ ) V_x(\tau) . When the switches are open, the lower part of the network is a standard R C RC -/ R L RL -circuit. For both circuits, the solution is well known: C : V x ( τ ) = V x ( 0 − ) e − τ R C = 1600 163 e − 1 = V 2 , L : V x ( τ ) = − R I l 1 ( 0 − ) e − R L τ = − 800 29 e − 1 = V 3 \begin{aligned} C:&& V_x(\tau) &= V_x(0^-)e^{-\frac{\tau}{RC}}=\frac{1600}{163}e^{-1}=V_2,&&&&& L:&& V_x(\tau)&= -RI_{l1}(0^-)e^{-\frac{R}{L}\tau}=-\frac{800}{29}e^{-1}=V_3 \end{aligned} Assuming we have to add the absolute values, we get the answer ∣ V 1 ∣ + ∣ V 2 ∣ + ∣ V 3 ∣ ≈ 23.4 |V_1|+|V_2|+|V_3|\approx \boxed{23.4}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...