A beautiful construction
In the following figure A E = A D = D C = A C = F G = 1
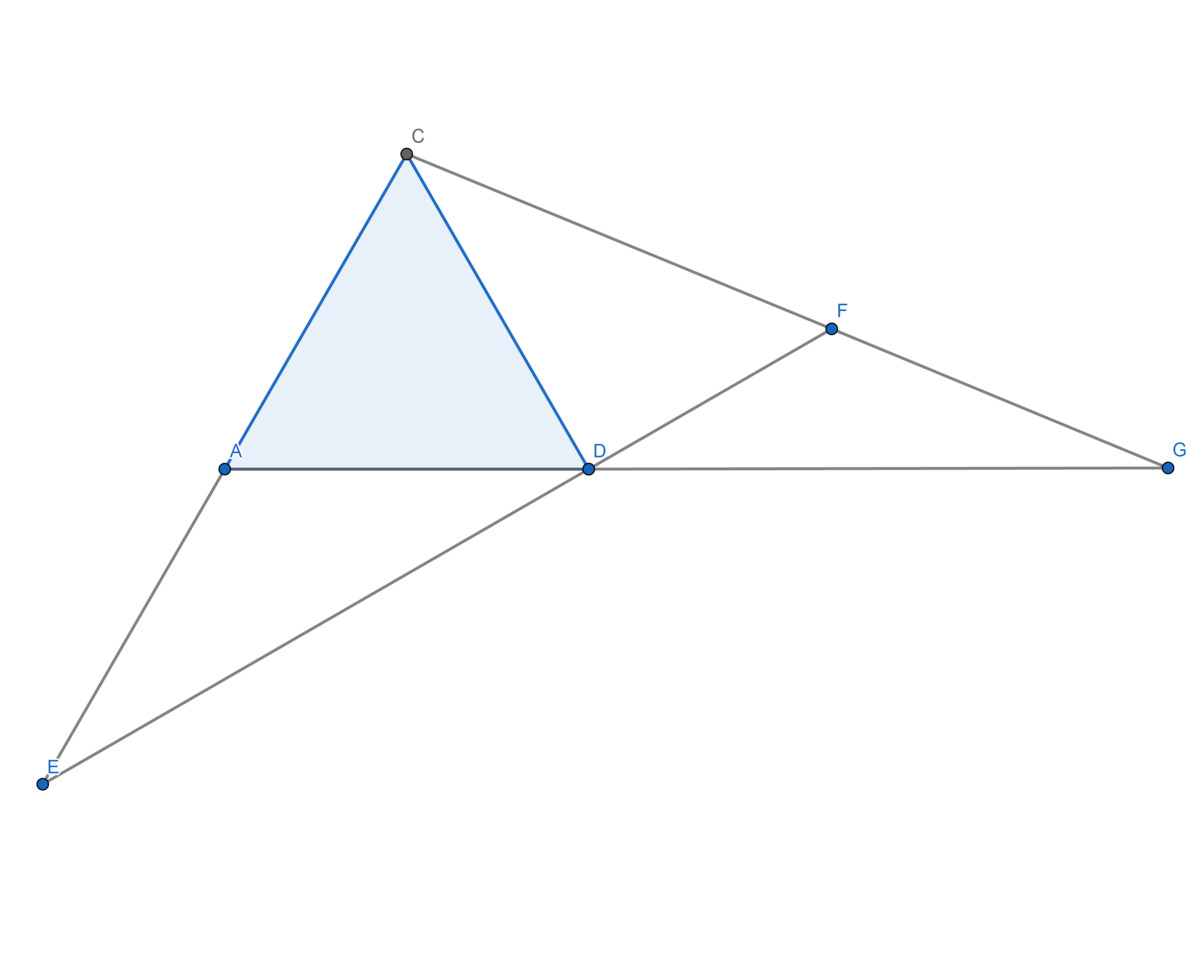
What is the length of C F ?
The answer is 1.25992.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
That explains why it was so hard to construct with straightedge and compass.
By Menelaus' Theorem considering the transversal A D G of the triangle C E F , A E C A × D F E D × G C F G = − 1 (here lengths are signed). Thus 1 × C F 2 − 1 3 × C F + 1 1 = 1 and hence C F 2 − 1 ( C F + 1 ) = 3 , and so C F is a positive real root of the equation ( x 2 − 1 ) ( x + 1 ) 2 − 3 x 4 + 2 x 3 − 2 x − 4 ( x + 2 ) ( x 3 − 2 ) = 0 = 0 = 0 and so C F = 3 2 .
L e t D F = X . F r o m t h e g i v e d a t a , Δ C A D i s 1 − 1 − 1 , ∴ ∠ s C A D = A D C = 6 0 o . S o ∠ D A E = 1 2 0 o , b u t A E = A D , ∴ i n Δ A E D , ∠ F D G = E D A = 3 0 o , a n d ∠ C D F = 9 0 o . r t . ∠ Δ C D F , ∠ F C D = a t a n X . U s i n g S i n e L a w i n Δ F D G , 1 / s i n 3 0 = X / s i n D G F , ∴ ∠ D G F = a s i n ( X / 2 ) . I n Δ C D G , ∠ s D G F + F C D = 1 8 0 − 1 2 0 = 6 0 o S o l v i n g a s i n ( X / 2 ) + a t a n X = 6 0 o b y t r i a l a n d e r r o r , w e g e t X = . 7 6 6 . ⟹ C F = 1 2 + . 7 6 6 2 = 1 . 2 5 9 6 6 .
Letting C F = x , and using the Law of Sines, we solve for x
x 2 − 1 S i n ( A r c C s c ( x ) − 6 π ) = 1 S i n ( 6 π )
which delivers x = 1 . 2 5 9 9 2
Considering that ∠ C D F = 2 π , sin ∠ D F C = C F C D = x 1
Let D G = y . Employing the sine law, we see that for triangle D F G :
1 sin 6 π = y sin ∠ D F G
2 1 = y sin ( π − ∠ D F C
2 1 = y sin ∠ D F C
2 1 = y x 1
2 1 = x y 1
x y = 2
Employing the cosine law, we see that for triangle C D G :
( x + 1 ) 2 = 1 2 + y 2 − 2 ( 1 ) ( y ) cos 3 2 π
x 2 + 2 x + 1 = 1 + y 2 − 2 y ( − 2 1 )
x 2 + 2 x = y 2 + y
x ( x + 2 ) = y ( y + 1 )
x ( x + x y ) = y ( y + 1 )
x x ( 1 + y ) = y ( y + 1 )
x 2 = y
x x 2 = x y
x 1 + 2 = 2
x 3 = 2
x = 3 2
With some angle chasing we can find out that ∠ B F G = 3 0 ° and ∠ C D G = 1 2 0 ° Let D F = y and C F = x
Observing that ∠ C D F = 9 0 ° we know from pytaghorean theorem that
1 2 + y 2 = x 2 and x > y > 0
Now, from law of sines in △ F D G
sin ( ∠ F G D ) y = sin ( 3 0 ° ) 1 ∴ y = 2 × sin ( ∠ F G D )
Then, law of sines in △ C D G
sin ( ∠ F G D ) 1 = sin ( 1 2 0 ° ) 1 + x ∴ x = 2 1 3 csc ( ∠ F G D ) − 1
putting al together and solving those equations we get the answer 3 2
It looks like you have a point B hiding under point D which makes it hard to read. I wonder if you can fix this? It would also be nice if your picture indicated which sides are equal to 1.
We first note that triangle A E D is isosceles with vertex angle 1 2 0 ∘ , so ∠ E D A = 3 0 ∘ , which then makes ∠ F D G = 3 0 ∘ and ∠ C D F = 9 0 ∘ .
Since triangle C D F is right, we know that sin θ = x 1 . Also, applying Sine Law to triangle D F G , we get
1 sin 3 0 ∘ 2 1 2 1 y = y sin α = y sin θ [ Because θ = 1 8 0 ∘ − α ] = x y 1 [ Using sin θ = x 1 ] = x 2
Now we use Cosine Law on triangle C D G :
( x + 1 ) 2 x 2 + 2 x + 1 x 4 + 2 x 3 + x 2 x 4 + 2 x 3 x 3 ( x + 2 ) x 3 x = 1 2 + y 2 − 2 ( 1 ) ( y ) cos 1 2 0 ∘ = 1 + x 2 4 + x 2 [ Now multiply by x 2 ] = x 2 + 2 x + 4 = 2 x + 4 = 2 ( x + 2 ) [ Since x cannot be - 2 , we can divide by ( x + 2 ) ] = 2 = 3 2 ≈ 1 . 2 5 9