A beautiful problem from a Hungarian competition
We need to fill each cell in a grid with a distinct integer from 1 to 36. There are two rules:
- Every pair of consecutive numbers are in adjacent cells that share an edge.
- Any two cells containing a multiple of 4 cannot share an edge nor a vertex.
Over all valid configurations, how many of the 36 cells could contain the number
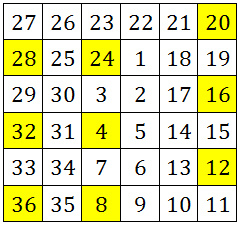
Note
: Below is a
grid adhering to the rules above.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We will prove that 3 6 can only be in a corner. It's easy to see that every even number will be placed on the same colour. We have nine numbers from
1
to
3
6
which have the
4
divisor:
4
,
8
,
1
2
,
1
6
,
2
0
,
2
4
,
2
8
,
3
2
,
3
6
. We can suppose that even numbers will be placed on the red cells. In the figure we dismembered the table to nine pieces of
2
×
2
square. There cannot be two-divisible by
4
-numbers in one
2
×
2
square, so in every
2
×
2
square there will be exactly one number which is divisible by
4
. The
6
×
6
grid has a rotational symmetry, so we can suppose that in the middle
2
×
2
square this number (which is divisble by
4
) is in the F cell. Then in the
A
,
B
,
C
,
E
,
G
,
I
,
J
,
K
cells there must not be a number, which is a multiply of
4
. So in the
I
J
M
N
2
×
2
square the number, which is divisible by
4
, can only be in cell
N
(because
M
is a blue cell). Similarly in the
C
D
G
H
2
×
2
square the only possible place for the number, which is divisble by
4
, is cell
H
. Now we can see that in the
K
L
O
P
2
×
2
square the number, which is a multiply of
4
, can't be in
K
,
L
,
O
cells, so it must be on the
P
cell. We will show that the only number, which can be on the
P
cell, is
3
6
. If it were different (for example
4
∗
a
) then
1
<
4
∗
a
<
3
7
would be true, so
4
a
+
2
and
4
a
−
2
would have to be placed on the grid. These numbers can't be on the
N
,
H
cells (because
4
is not a divisor of
4
a
−
2
and
4
a
+
2
)
, so in cell
K
there would have to be
2
numbers, which would not be possible. So
3
6
has to be in a corner, and there are
4
corners. A possible numbering:
It's easy to see that every even number will be placed on the same colour. We have nine numbers from
1
to
3
6
which have the
4
divisor:
4
,
8
,
1
2
,
1
6
,
2
0
,
2
4
,
2
8
,
3
2
,
3
6
. We can suppose that even numbers will be placed on the red cells. In the figure we dismembered the table to nine pieces of
2
×
2
square. There cannot be two-divisible by
4
-numbers in one
2
×
2
square, so in every
2
×
2
square there will be exactly one number which is divisible by
4
. The
6
×
6
grid has a rotational symmetry, so we can suppose that in the middle
2
×
2
square this number (which is divisble by
4
) is in the F cell. Then in the
A
,
B
,
C
,
E
,
G
,
I
,
J
,
K
cells there must not be a number, which is a multiply of
4
. So in the
I
J
M
N
2
×
2
square the number, which is divisible by
4
, can only be in cell
N
(because
M
is a blue cell). Similarly in the
C
D
G
H
2
×
2
square the only possible place for the number, which is divisble by
4
, is cell
H
. Now we can see that in the
K
L
O
P
2
×
2
square the number, which is a multiply of
4
, can't be in
K
,
L
,
O
cells, so it must be on the
P
cell. We will show that the only number, which can be on the
P
cell, is
3
6
. If it were different (for example
4
∗
a
) then
1
<
4
∗
a
<
3
7
would be true, so
4
a
+
2
and
4
a
−
2
would have to be placed on the grid. These numbers can't be on the
N
,
H
cells (because
4
is not a divisor of
4
a
−
2
and
4
a
+
2
)
, so in cell
K
there would have to be
2
numbers, which would not be possible. So
3
6
has to be in a corner, and there are
4
corners. A possible numbering: