A beautifully ugly equation

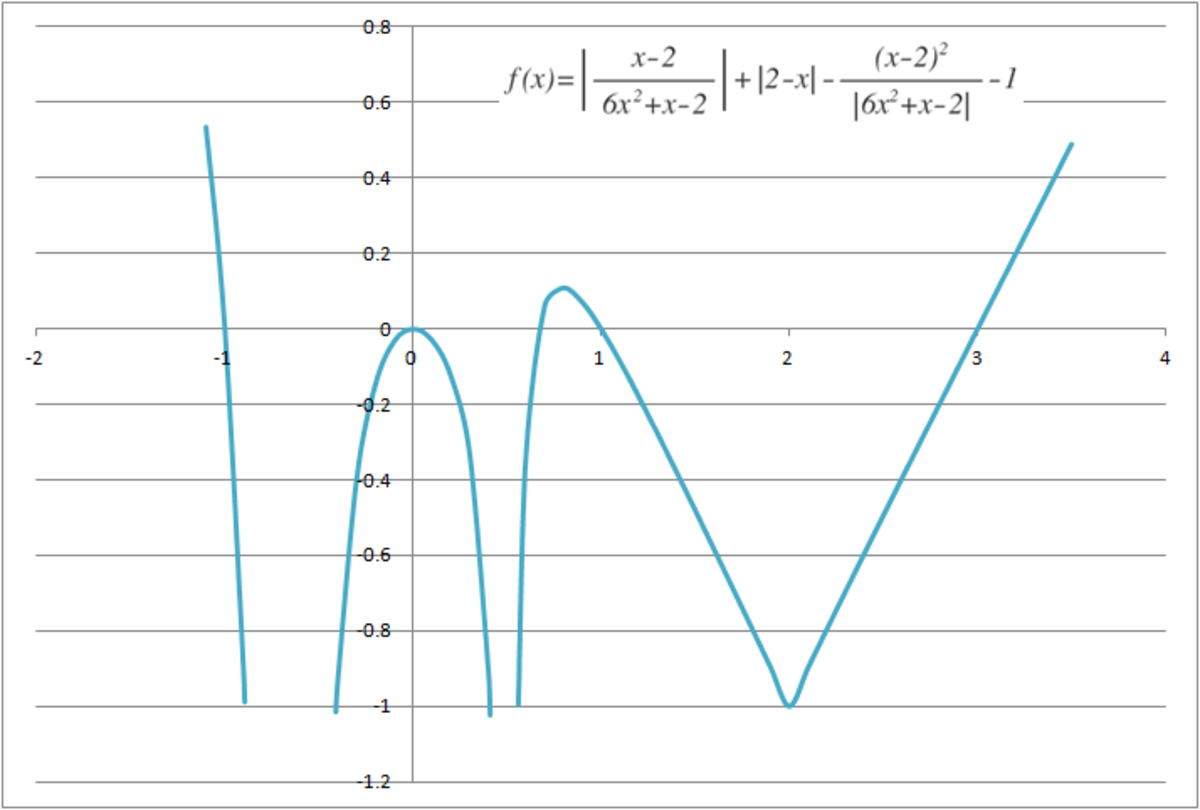
The given equation can be rewritten as $\left| \dfrac{x-2}{6x^2+x-2}\right|+|x-2|=\dfrac{|x-2| \cdot |x-2|}{|6x^2+x-2|}+1$ Let

$|x-2|=a$ and

$\left| \dfrac{x-2}{6x^2+x-2}\right| =b$

Now the expression can be rewritten in terms of $a$ and $b$ as $\Rightarrow b+a=ab+1$ $\Rightarrow (a-1)(b-1)=0$ $\Rightarrow a=1, b=1$

• Case 1

$|x-2|=1\Rightarrow x=1,3$

• Case 2

$\left| \dfrac{x-2}{6x^2+x-2}\right|=1$

$\Rightarrow\dfrac{x-2}{6x^2+x-2}=\pm 1$ $\Rightarrow x=-1,0, \frac{2}{3}$

$\Rightarrow \boxed{x=-1,0, \frac{2}{3},1,3}$

The solution can be obtained by plotting the curve as follows (if it is not considered cheating):