A better approximate Pythagoras

Calculus Level 5

In the problem Approximate Pythagoras you can see that adding one-half of the shorter leg to the longer leg of a right triangle gives a pretty good estimate for the hypotenuse. b + a / 2 ≈ c b+a/2 \approx c

Now the task is to improve the parameter one-half

Find x x on the interval [ 0 , 1 ] [0,1] such that the maximum percentage error (larger or smaller) of using x a + b xa+b to approximate a 2 + b 2 \sqrt{a^{2}+b^{2}} is minimized.


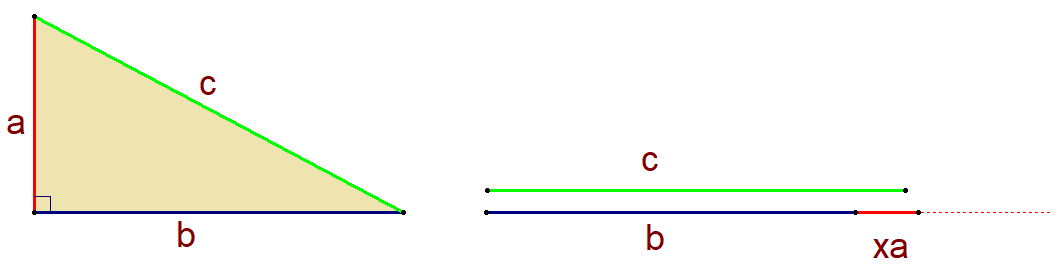
The answer is 0.3363572758.

Jeremy Galvagni by Jeremy Galvagni , 48, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Jeremy Galvagni
Oct 9, 2018

Define the function f ( x ) = x + a 1 + x 2 f(x)= \frac{x+a}{\sqrt{1+x^{2}}} as the proportional error. 1 − f ( x ) 1-f(x) is the percentage difference.

Using the derivative you can show the maximum value of f f occurs at x = 1 a x=\frac{1}{a} and f ( 1 a ) = 1 + a 2 f\left(\frac{1}{a}\right)=\sqrt{1+a^{2}} which tends to 1 1 as x x goes to infinity.

The minimum of f f is 1 1 if a ≥ 2 − 1 a \ge \sqrt{2}-1 otherwise it's f ( 1 ) = 1 + a 2 f(1)=\frac{1+a}{\sqrt{2}}

We seek to minimize the maximum error so that the error from being over is the same as the error from being under: f ( 1 a ) − 1 = 1 − f ( 1 ) f\left(\frac{1}{a}\right) - 1 = 1 - f(1) or 1 + a 2 + 1 + a 2 = 2 \sqrt{1+a^{2}}+\frac{1+a}{\sqrt{2}}=2

Wolfram alpha gives the solution x = 1 − 2 2 + 2 4 − 2 2 ≈ 0.3363572758 x=1-2\sqrt{2}+2\sqrt{4-2\sqrt{2}} \approx \boxed{0.3363572758}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...