A Block of Wood
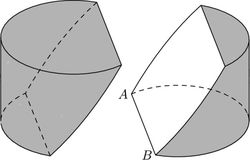A block of wood has the shape of a right circular cylinder with radius 6 and height 8, and its entire surface has been painted blue. Points A and B are chosen on the edge of one of the circular faces of the cylinder so that arc AB on that face measures 120 degrees. The block is then sliced in half along the plane that passes through point A, point B, and the center of the cylinder, revealing a flat, unpainted face on each half.
The area of one of these unpainted faces is , where are integers and is not divisible by the square of any prime. Find .
The answer is 53.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the points where the plane intersects the top face of the cylinder as C and D, and the center of the cylinder as O, such that C,O, and A are collinear. Let T be the center of the bottom face, and M the midpoint of AB. Then OT=4, TM=3(because of the 120 degree angle), and so OM=5.
Project C and D onto the bottom face to get X and Y, respectively. Then the section ABCD (whose area we need to find), is a stretching of the section ABXY on the bottom face. The ratio of stretching is OM/TM = 5/3, and we do not square this value when finding the area because it is only stretching in one direction. Using 30-60-90 triangles and circular sectors, we find that the area of the section 18* sqrt(3) + 12 * pi. Thus, the area of section 20 * pi + 30* sqrt(3), and so our answer is 20 + 30 + 3 = 053