A board

Classical Mechanics Level 3

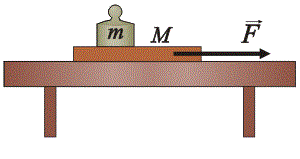
There is a board with mass M = 1 kg M = 1 \text{ kg} on a desk and on the board a weight with mass m = 2 kg m = 2 \text{ kg} . The coefficient of friction between the desk and the board is f 1 = 0.35 f_1 = 0.35 and the coefficient of static friction between the weight and the board is f 2 = 0.5. f_2 = 0.5. What is the minimal force one has to exert on the board to pull it out from under the weight?

Details and assumptions:

  • g = 9.81 m/s 2 g = 9.81 \text{ m/s}^2
  • Choose the closest option.
38 N 38 \text{ N} 18 N 18 \text{ N} 30 N 30\text{ N} 15 N 15 \text{ N} 25 N 25 \text{ N}

Munem Shahriar by Munem Shahriar , 18, Bangladesh

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Darryl Dennis
Mar 9, 2018

Weight m would be accelerated horizontally at the same acceleration rate as the board M that it is sitting on as long as the friction between the weight and the board is large enough to produce the horizontal force on the weight required to accelerate the mass of that weight at the acceleration rate of the board. The force required to slip or move the weight on the board could be calculated by f=ma however, in this problem, the value of interest is the acceleration required , by both the board and the weight, to cause the weight to begin to slip on the board.

The equivalent horizontal acceleration of the weight duo to gravitational pull g = 9.81 m/s 2 g= 9.81 \text{m/s}^2 .

The minimum horizontal acceleration of the board and the weight together to slip the weight on the board would be f 2 ∗ g = 0.5 ∗ 9.81 = 4.905. m / s 2 f_2 * g = 0.5 * 9.81= 4.905.{m/s}^2 . At any acceleration rate below 4.9005 m/s/s the weight would sit still relative to the board because the friction between the board and the weight is greater than the force required to accelerate the weight. In the event that the board is accelerating at any rate greater than 4.9005 m/s/s the friction between the board and the weight would not be sufficient to accelerate the weight at the same rate as the board and the weight would slip on the board.

How much force would be required to accelerate the weight sitting on the board at 4.9 m / s 2 4.9 { m/s}^2 .

The force would have to accelerate the mass of the board and the weight F = m a = ( 1 k g + 2 k g ) ∗ 4.905 = 14.715 N F=ma=(1 kg + 2kg) * 4.905 = 14.715 N .

The force required must also overcome friction between the board and the table. f 1 ∗ g ∗ ( m + M ) = 0.35 ∗ 9.81 ∗ ( 1 + 2 ) = 10.3005 N f_1*g*(m+M)=0.35*9.81*(1+2)= 10.3005N .

Total force required 14.715 N + 10.3005N = 25.0 N.

1 Helpful 1 Interesting 1 Brilliant 1 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...