A Box and a Wedge (ITA-IME Brazil)

Classical Mechanics Level 2

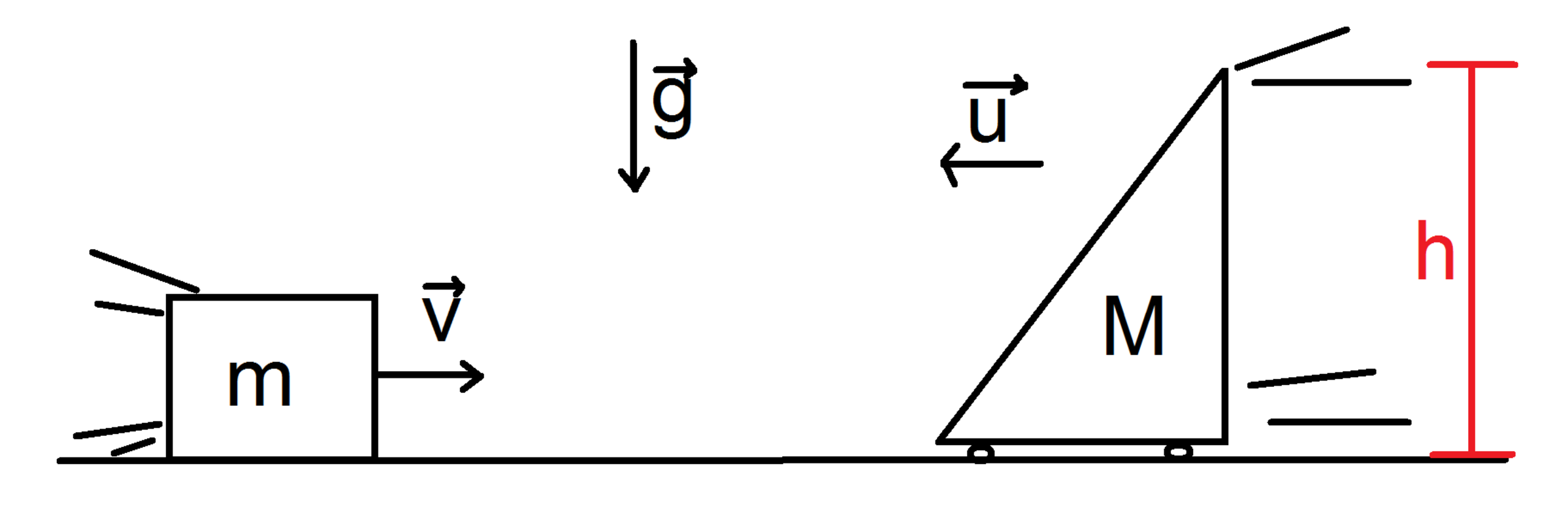
A box of mass m moves with speed v toward a wedge of mass M, which moves with speed u in the opposite direction. The box slides on the frictionless wedge and reaches a height h. There is no friction between the ground and the box. Find h.

(M/m+M)(u-v)²/2g (M/m-M)(u+v)²/2g (M/m-M)(u-v)²/2g (M/m+M)(u+v)²/2g

Samuel Nascimento by Samuel Nascimento , 24, Brazil

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Samuel Nascimento
Jul 17, 2019

In physics, the reduced mass (m') is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. It is a quantity which allows the two-body problem to be solved as if it were a one-body problem. Note, however, that the mass determining the gravitational force is not reduced.

m' = m M m + M \frac{mM}{m+M}

Let v' be the relative velocity between the box and the wedge: (v' = u+v)

From the conservation of mechanical energy, we have:

m ′ ( v ′ ) ² 2 \frac{m'(v')²}{2} = mgh

h = m ′ ( v ′ ) ² 2 m g \frac{m'(v')²}{2mg}

h = m M ( u + v ) ² 2 m g ( m + M ) \frac{mM(u+v)²}{2mg(m+M)}

h = M ( u + v ) ² 2 g ( m + M ) \frac{M(u+v)²}{2g(m+M)}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...