A Box of Rati-O's

Geometry Level 3

Rectangle $\mathbb{A}$ is inscribed in rectangle $\mathbb{B}$ , so that each of the vertices of $\mathbb{A}$ lies on a different side of $\mathbb{B}$ .

The length-to-width ratio for $\mathbb{A}$ is 2:1, and the length-to-width ratio for $\mathbb{B}$ is 3:2.

Find the ratio of the area of $\mathbb{A}$ to the area of $\mathbb{B}$ .

If your answer is $a: b$ , where $a$ and $b$ are positive coprime integers, enter $a+b$ as your answer.

The answer is 44.

1 solution

Calvin Lin Staff
May 18, 2015

[This is not a complete solution]

Hint: Show that the green triangle and yellow triangle are similar.

The solution follows easily after that.

WLOG let Rectangle A be 1 X 2. Label segments of Rectangle B w, x, y, and z, with the goal of parameterizing all of them in terms of x:

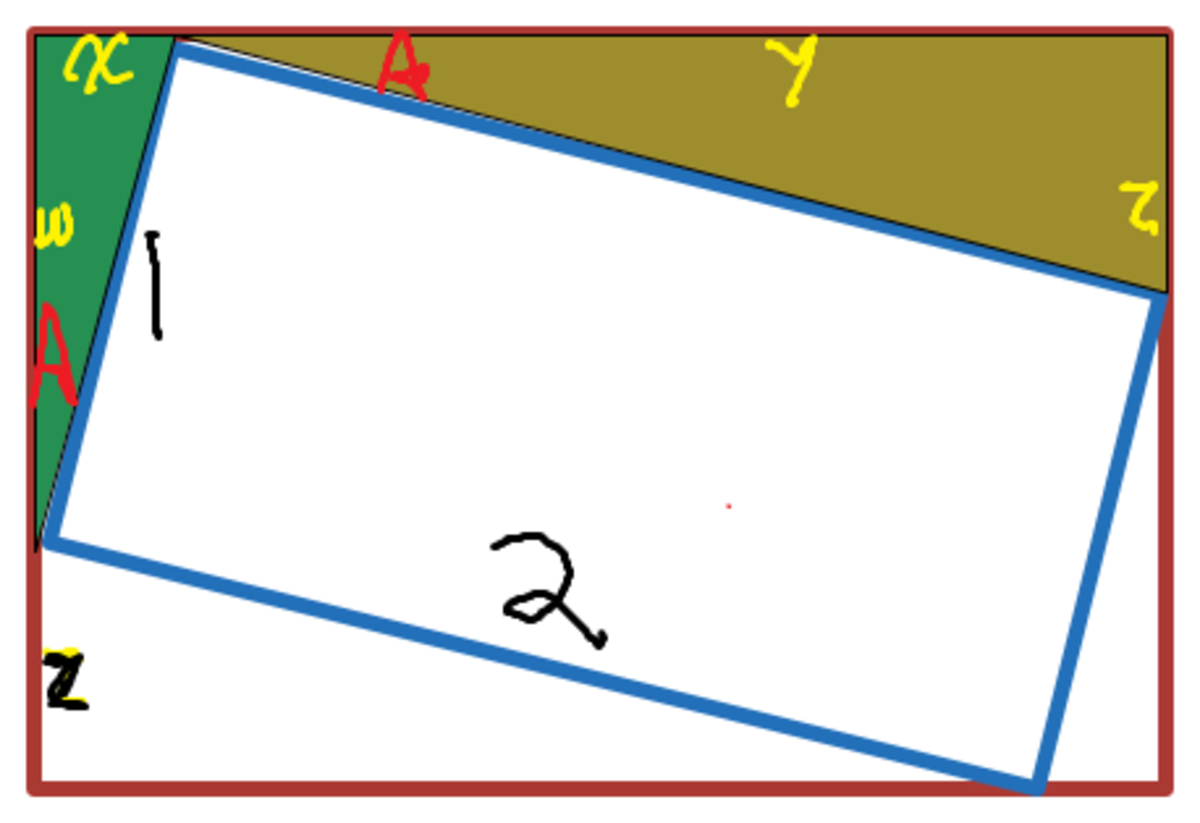
Since $\sin{A} = \frac{x}{1} = \frac{z}{2}, z = 2x.$ Since $\cos{A} = \frac{w}{1} = \frac{y}{2}, y = 2w.$

Now $\frac{3}{2} = \frac{x+y}{w+z} = \frac{x + 2w}{w + 2x} \mbox{, so } 3w + 6x = 2x + 4w \mbox{, which yields } 4x = w$ .

By the Pythagorean Theorem, $1 = x^2 + w^2 = x^2 + (4x)^2 \mbox{, so } x = \frac{1}{\sqrt{17}}$ .

Then $(w, x, y, z) = (4x, x, 8x, 2x) = \left( \frac{4}{\sqrt{17}}, \frac{1}{\sqrt{17}}, \frac{8}{\sqrt{17}}, \frac{2}{\sqrt{17}} \right)$ , which is enough to answer the question.

Tim Cieplowski - 6 years ago

Looks good.

For completeness, you should also explain why those triangles are similar, or at least why the 2 angles marked A are the same.

Calvin Lin Staff - 6 years ago

A Box of Rati-O's

The answer is 44.

1 solution

0 pending reports