A Bright Library

Consider a light bulb on the top of a library. It is 2 0 m above the ground and, horizontally, 5 m from a wall. Consider that the recipe that contains the light bulb is a conical frustum with a greater diameter of 8 cm , height of 2 cm and smaller diameter of 4 cm . Take the recipe to be opaque to light. How far from the ground, in meters, is the highest point of the wall that can be illuminated by the light bulb?
Details and Assumptions :
-
The light bulb is right in the middle of the recipe's smaller base. Take the bulb to be a punctate body.
-
The smaller diameter is the diameter of the frustum's smaller base, and the greater diameter is the diameter of the frustum's greater base.
The answer is 17.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I think it can solved in a easier way From figure, \tan \phi = \frac{h}{r+x} = \frac{20-H}{5} So, \frac{2}{4} = \frac{20-H}{5} 20-H = 2.5 H = 17.5m
Request: I've written the solution from app. I couldn't upload a photo or format it properly. If someone can format this properly, I'll be very much thankful
It is easier to solve this problem by drawing, so I'll do the calculations based on the photos below. The light ray that is represented is inciding on the maximum point of the recipe in order to get out of it and iluminate the wall. As we are thinking of a point, we can turn this problem into a bidimensional situation (shown on the second picture). Let
R
be the greater radius and
r
be the smaller radius. We can see that there is a proportion of
R
r
=
2
1
, so the "ghost" part's height is half of the total height. As the frustum's height is the other half, so the "ghost" part's height is also
h
′
=
2
c
m
. Now, we can state that
r
=
h
′
, so the triangle ABC is isosceles, which implies that
θ
=
4
5
°
. In order to calculate the value of
x
(which is shown on the third picture), we can use theta's tangent, which is 1. So
x
h
=
1
⇒
h
=
x
. Now, we can say that
tan
ϕ
=
(
r
+
x
)
h
⇒
tan
ϕ
=
2
h
h
⇒
tan
ϕ
=
2
1
. Note that
(
r
+
x
)
=
2
h
because
x
=
h
=
h
′
=
r
. The highest point of the wall that can be iluminated by the light bulb is
H
meters above the ground. So, as it is shown on the fourth picture,
tan
ϕ
=
5
(
2
0
−
H
)
⇒
2
(
2
0
−
H
)
=
5
⇒
H
=
1
7
.
5
m
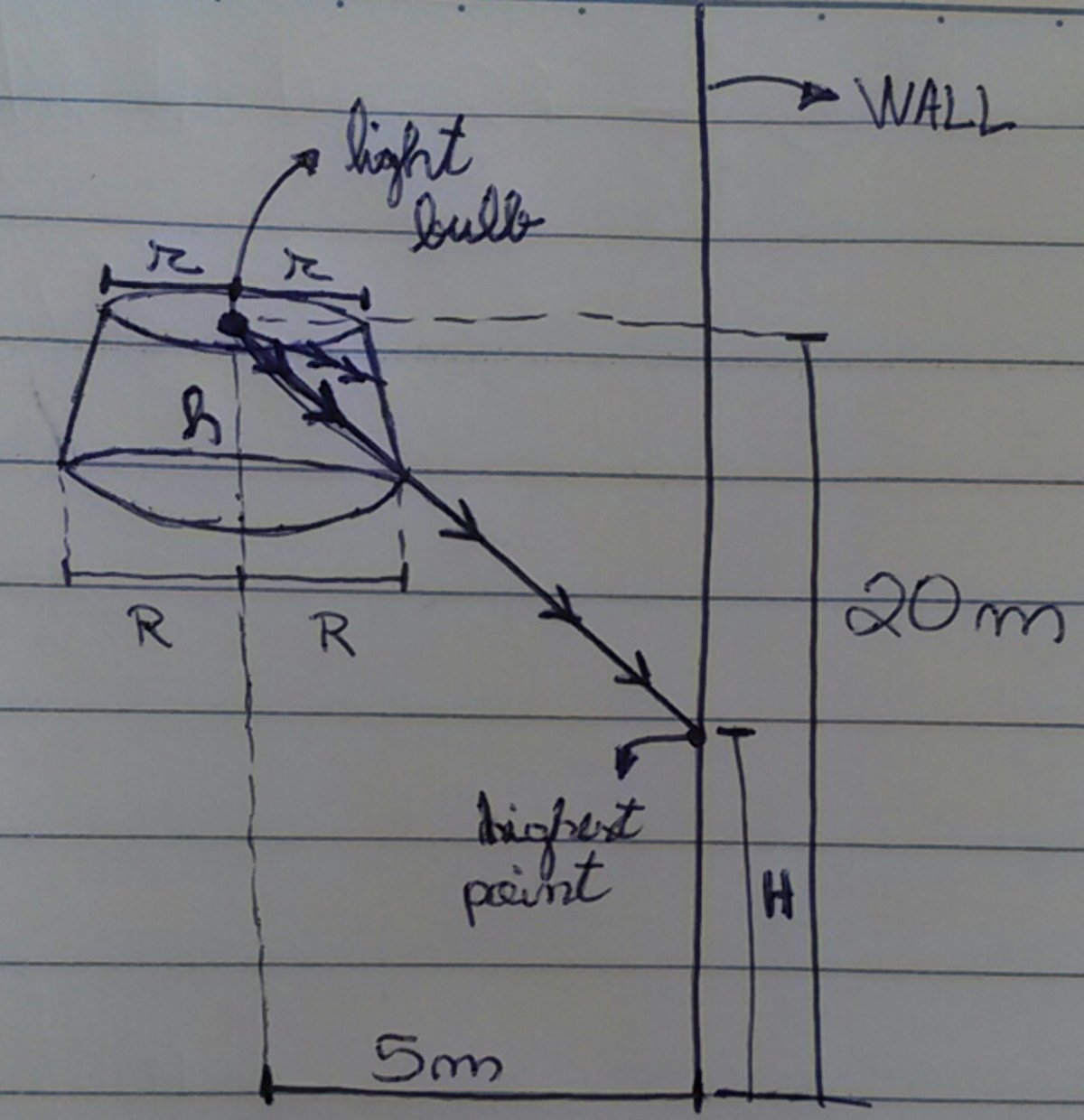
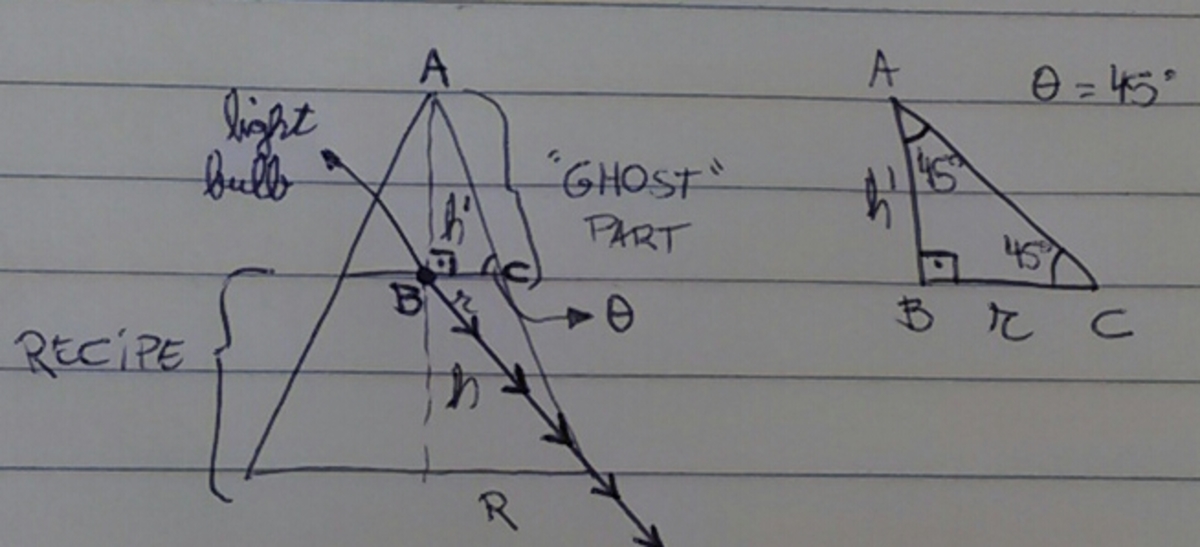
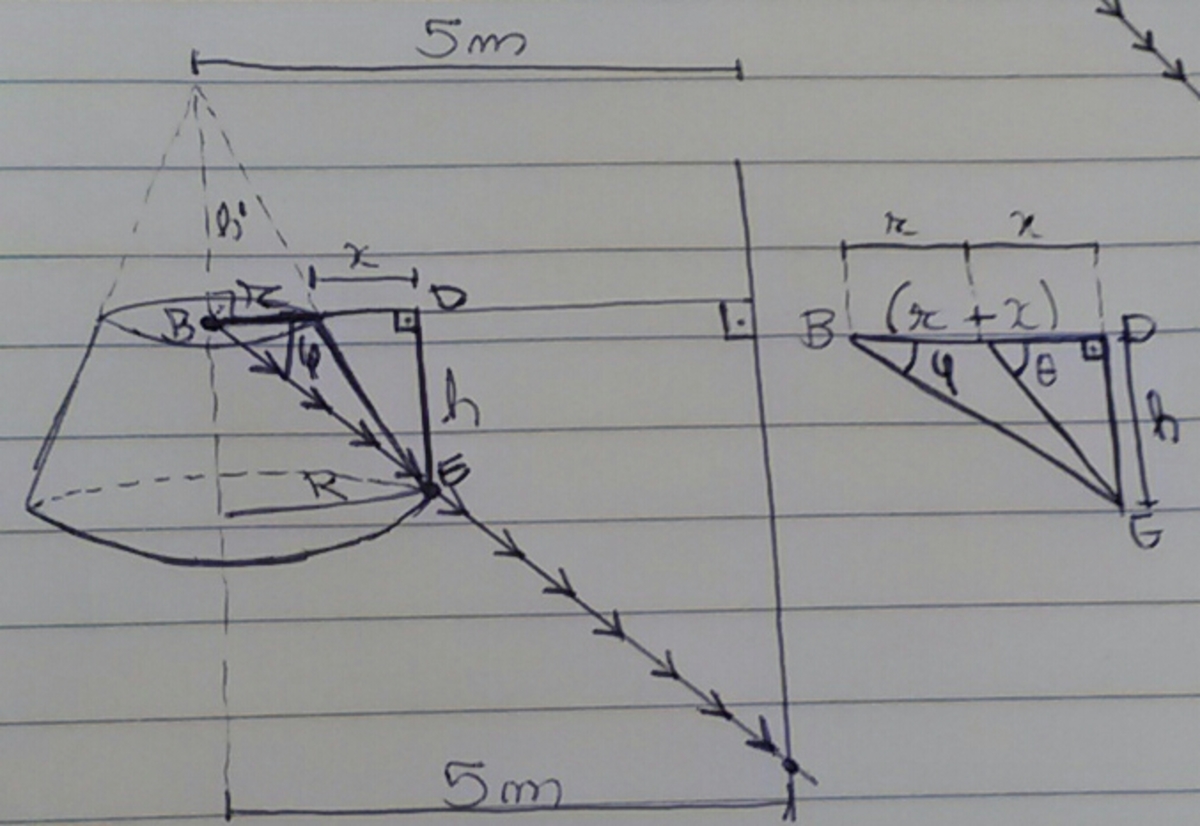
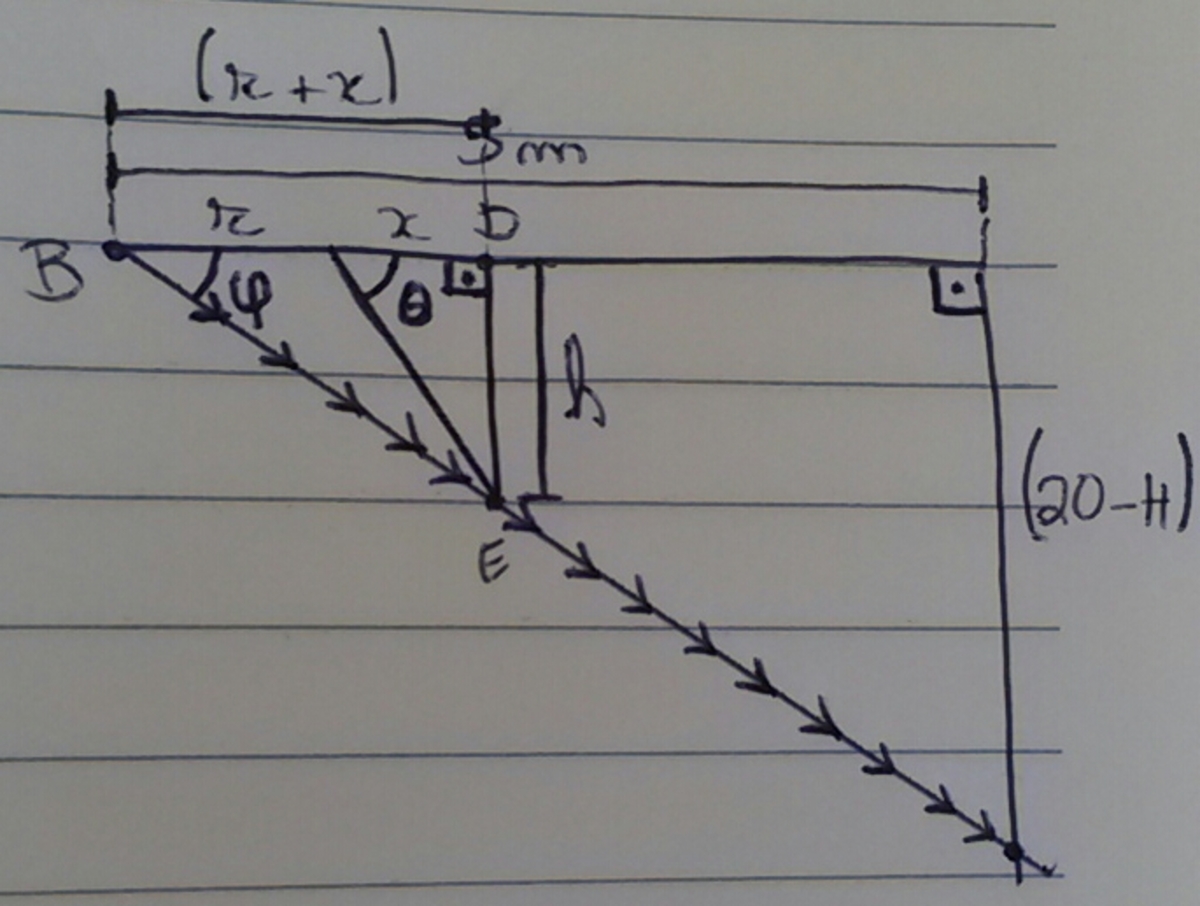
The highest light on the wall lies on the line from the bulb through the bottom of the conical frustrum.
The slope of this line is horizontal vertical = 4 cm 2 cm . Therefore the vertical distance of the highest light below the light bulb is 5 m × 4 cm 2 cm = 2 . 5 m . The height above the wall is 2 0 − 2 . 5 = 1 7 . 5 m .