A bucket with mass m2 and a block with mass m1 are hung on a pulley system.
A bucket with mass
and a block with mass
are hung on a pulley system. Find the ratio of magnitude of the acceleration of the bucket and the block. The bucket moves up and the block moves down.
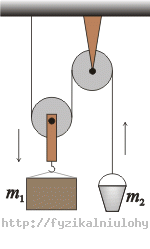
asume that the pulleys are massless and there is no friction.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Forces that affect the bucket m 2 :
1 . F G 2 … w e i g h t
2 . T 1 … t e n s i o n f o r c e by which the rope affects the bucket
Forces that affect the block m 1 :
1 . F G 1 … w e i g h t
2 . T 1 … t e n s i o n f o r c e by which the rope affects the block
3 . T 2 … t e n s i o n f o r c e by which the rope affects the block
The vector force equation for the bucket:
F G 2 + T = m 2 × a 2 ( 1 ) The vector force equation for the block:
F G 1 + T 1 + T 2 = m 1 × a 1 ( 2 )
We choose the y-axis the way it is marked on the picture.
We rewrite equations (1) and (2) to scalar form:
T − F G 2 = m 2 a 2 ( 3 ) F G 1 − T 1 − T ′ 2 = m 1 a 1 ( 4 )
Because we leave the mass of the pulley system and the rope out of account they have no moment of inertia and don’t affect the tension forces. The following holds for the magnitude of the tension forces:
∣ T ∣ = ∣ T 1 ∣ = ∣ T 2 ∣
We rewrite equations (3) and (4):
T − F G 2 = m 2 a 2 ( 5 ) F G 1 − 2 T = m 1 a 1 ( 6 )
Relation between the magnitudes of acceleration a 1 a n d a 2 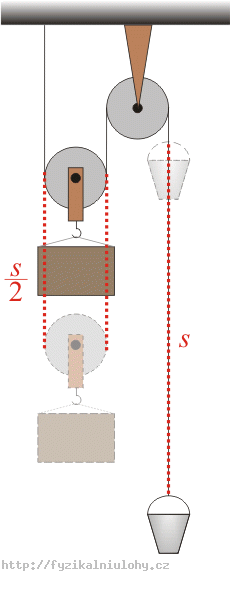
If the bucket goes up a distance s , the block goes down a distance 2 x
s = 2 1 a 2 t 2
2 s = 2 1 a 1 t 2
2 = a 1 a 2
a 2 = 2 a 1 ( 7 )