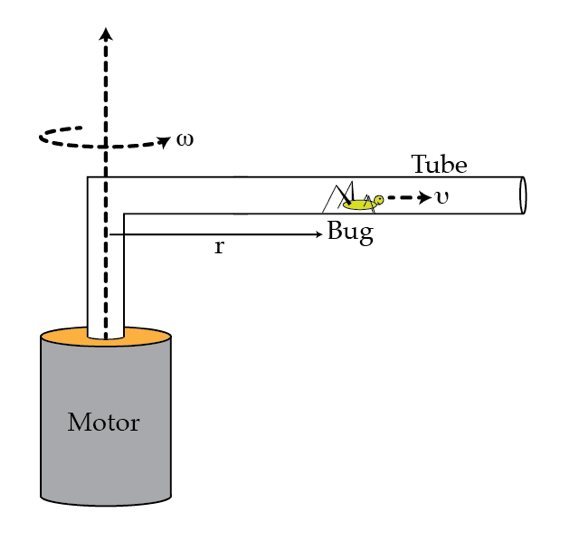
A bug in a rotating pipe

First, consider the case that the motor is inactive. Conservation of angular momentum implies that $|L| = |r \times p| = m \omega r^2$ is constant. We thus find that:

$\frac{d\omega}{dt} = \frac{d}{dt} \frac{L}{mr^2} = -\frac{2vL}{mr^3} = -\frac{2v \omega}{r}$

The corresponding reduction in (rotational) energy is:

$\frac{dE}{dt} = \frac{d}{dt} \frac12 m \omega^2 r^2 = m \omega r^2 \frac{d\omega}{dt} = -m \omega r^2 \frac{2v \omega}{r} = -2m \omega^2 vr$

In order to keep w constant, the motor must thus counter this, i.e.

$P = -\frac{dE}{dt} = 2mw²vr$

Initial mechanical energy: E 0 = \frac {1}{2} \times _m \times [ v ^2 + (wr) ^2] + \frac {1}{2} \times m r ^2 \times _w ^2

After the bug crawls a very small distance d : E f = \frac {1}{2} \times _m \times [ v ^2 + w^2 \times ( r + d )^2] + \frac {1}{2} \times m ( r + d )^2 \times w ^2

( r + d )^2 can be written as : r^2 \times (1 + \frac { d }{ r })^2, using the approximation (1 + x )^n ~= 1 + nx (When 1 >>> n)

We have that: E f = \frac {1}{2} \times _m \times [ v ^2 + w ^2 \times ( r ^2 + 2 \times r \times d )] + \frac {1}{2} \times m ( r ^2 + 2 \times r \times d ) \times w ^2

E f - E 0 = 2 \times \frac {1}{2} \ times 2 \times m \times w ^2 \times r \times d = 2

Since the energy difference is caused by the motor, P m \times _t = E f - E 0, as d = v \times t we have that:

P m \times _t = 2 \times m \times w ^2 \times r \times v \times t

P m = 2 \times _m \times w ^2 \times r \times v .

So C = 2.

Since the tube is massless, the only mass required in the calculation of $I$ (moment of inertia) is the mass of the bug. For a point mass, the moment of inertia is given by $I=mr^2$ , where $r$ is the distance of the point mass from the axis of rotation.

The kinetic energy of the system is given by $E=I\omega^2=mr^2\omega^2$ . However, the question asks for power and the reason for this is that the amount of energy needed changes as the bug walks down the tube. Realizing that $v=\frac{dr}{dt}$ and $P=\frac{dE}{dt}$ , we have that $P=\frac{d}{dt}mr^2\omega^2=m\omega^2\cdot2r\frac{dr}{dt}=2m\omega^2vr$ . Thus the requested answer is $C=\boxed2$ .

The instantaneous power in rotational systems is given by $\mathbf{\tau} \cdot \mathbf{\omega}$ , since power is $\mathbf{F} \cdot \mathbf{v}$ .

The torque is the time derivative of the angular momentum: $\mathbf{\tau} = \frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}$

The angular momentum in this case is $\mathbf{L} = \mathbf{r} \times \mathbf{p} = r m v_{rot} = m r^2 \omega$ . The last step drops the vector notation; all angular momenta and torques in this problem are along the rotational axis, as you can verify.

Notice that $L$ depends on $r$ . As the bug crawls along the pipe, it will change the angular momentum, exerting a torque on the system. What is the magnitude of that torque?

$\tau = \frac{\mathrm{d}L}{\mathrm{d}t} = \frac{\mathrm{d}(m r^2 \omega)}{\mathrm{d}t} = m \omega \frac{\mathrm{d}(r^2)}{\mathrm{d}t} = m \omega (2 r \frac{\mathrm{d}r}{\mathrm{d}t}) = 2 m \omega r v$

The third step was legal because we are assuming that $\omega$ is constant. The fourth step is just the chain rule of calculus. The fifth step is true because $\frac{\mathrm{d}r}{\mathrm{d}t}$ means "how fast the bug is changing its radius," which is defined as $v$ .

To keep the system rotating at constant angular speed, the motor needs to apply an equal and opposite torque.

So the power expended by the motor is $\tau \omega = 2 m \omega^2 v r$ .

Probably the easiest way to solve this problem is by looking at the angular momentum of the system $L=I\omega$ from which we can determine the torque developed by the motor $\tau= \frac{d L}{dt}=\omega \frac{d I}{dt}= \omega \frac{ d (mr^{2})}{dt}= 2 m \omega r \frac{dr}{dt}=2 m \omega v r.$ In the last step we made use of the fact that the moment of inertia of the system with respect to the vertical axis is $I=m r^{2}$ . Now, the power developed by the motor can be found using the formula $P_{m}= \tau \omega$ which yields $P_{m}= 2 m \omega^{2} v r \longrightarrow C=2.$ Another solution (which requires more thinking) is the following: Let us look at the kinetic energy of the system which can be written as $K=\frac{m}{2}(v_{r}^{2}+v_{t}^{2})=\frac{m}{2}(v^{2}+\omega^{2} r^{2}).$ Differentiating this expression we obtain $\frac{dK}{dt}=m \omega^{2} v r$ which suggests the incorrect answer $C=1$ . Well, we need to solve this "paradox". The answer lies in the fact that energy is dissipated in the system. There must be friction between the bug and the pipe, otherwise the bug would not be able to keep a constant speed relative to the pipe (it would accelerate). The force of friction can be found from Newton's second law; it must be equal to the centrifugal force. That is $f=m a_{c}= m \omega^{2} r$ Now, the power developed by the force of friction is just $P_{f}=\vec{f}\cdot \vec{v}=- m \omega^{2} v r.$ Now we can apply energy conservation and write $P_{m}+P_{f}=\frac{dK}{dt} \longrightarrow P_{m}=2 m \omega^{2} v r.$ Thus we obtain the correct answer $C=2.$

$\tau =\frac{d\vec{L}}{dt}=\frac{\mathrm{d} }{\mathrm{d} t}I\omega =\omega \frac{\mathrm{d} }{\mathrm{d} t}mr^{2}=2m\omega vr$

$P=\vec{F} \cdot \vec{v}= \vec{F} \cdot (\vec{\omega} \times \vec{r})= \vec{ \omega} \cdot ( \vec{r} \times\vec{F})= \vec{\tau} \cdot \vec{\omega }$

Since torque and angular velocity vectors are parallel: $P=\vec{\tau} \cdot \vec{\omega}=\tau\omega=2m\omega^{2}vr$

Hence, C=2