A calculus problem by Akshat Sharda
x → 0 lim ln ( 1 + x 3 ) sin − 1 x − tan − 1 x = A
Find the value of A 1 .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
We use the Taylor series for each term around 0 .
sin − 1 x = x + 6 x 3 + 4 0 3 x 5 + O ( x 6 )
tan − 1 x = x − 3 x 3 + 5 x 5 + O ( x 6 ) , so that
sin − 1 x − tan − 1 x = 2 x 3 + O ( x 5 ) . Also ,
l n ( 1 + x 3 ) = x 3 − 2 x 6 + 3 x 9 − . . . . = x 3 + O ( x 6 ) . It follows that
l i m x → 0 l n ( 1 + x 3 ) sin − 1 x − tan − 1 x = l i m x → 0 x 3 + O ( x 6 ) 2 x 3 + O ( x 5 ) = l i m x → 0 1 + O ( x 3 ) 2 1 + O ( x 2 ) = 1 + 0 2 1 + 0 = 2 1 .
Write the Taylor series expansion for all the functions around 0. Limit can be obtained as 1/2 easily
Well i dont remember the taylor series of inverse trigonometric functions. i remember only of sin , cos , tan and ln(1+x) .
I also used Taylor
Can you write a solution that is helpful to those who cannot solve it? Else I'm inclined to delete this solution to encourage others to contribute a relevant answer.
Well i did the long way. I Used L'Hospital's rule twice To get the answer 1/2
Can you write a solution that is helpful to those who cannot solve it? Else I'm inclined to delete this solution to encourage others to contribute a relevant answer.
Log in to reply
L'hospital's rule is the key behind my solution . just you need to differentiate twice and put in appropriate value
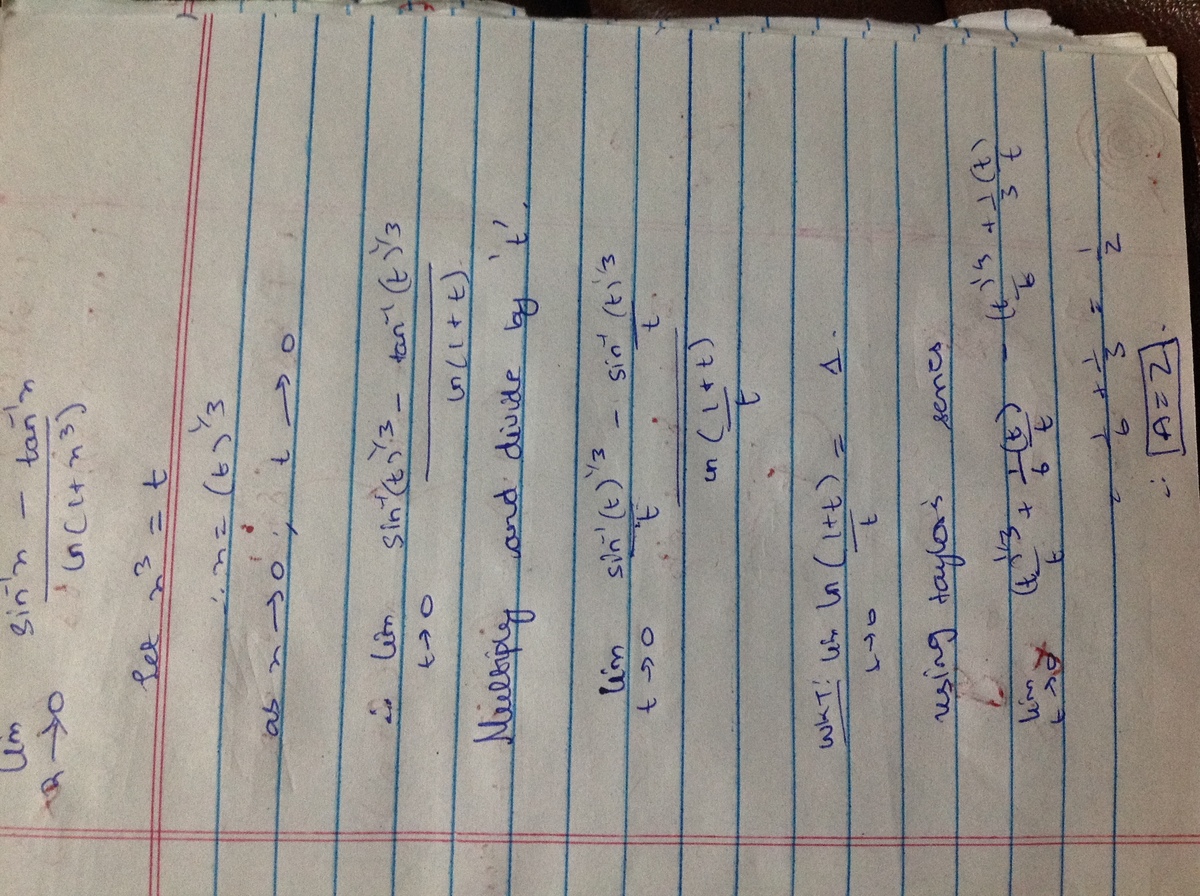
x → 0 lim ln ( 1 + x 3 ) ( sin − 1 x − tan − 1 x )
= x → 0 lim x 3 ( sin − 1 x − tan − 1 x ) ⋅ ln ( 1 + x 3 ) x 3
= x → 0 lim x 3 ( tan − 1 ( 1 − x 2 x ) − tan − 1 x ) ⋅ 1
= x → 0 lim x 3 ⎝ ⎛ tan − 1 ( 1 + 1 − x 2 x 2 ) ( 1 − x 2 x − x ) ⎠ ⎞
= x → 0 lim x 3 ( tan − 1 ( ( 1 − x 2 + x 2 ) ( x − x 1 − x 2 ) ) )
= x → 0 lim ( 1 − x 2 + x 2 ) ( x − x 1 − x 2 ) ( tan − 1 ( ( 1 − x 2 + x 2 ) ( x − x 1 − x 2 ) ) ) ⋅ x 3 ( 1 − x 2 + x 2 ) ( x − x 1 − x 2 )
= x → 0 lim 1 ⋅ x 3 ( 1 − x 2 + x 2 ) ( x − x 1 − x 2 )
= x → 0 lim x 2 ( ( 1 − x 2 + x 2 ) ( 1 − 1 − x 2 ) )
= x → 0 lim x 2 ( ( 1 − x 2 + x 2 ) ( 1 − 1 − x 2 ) ⋅ ( 1 + 1 − x 2 ) ( 1 + 1 − x 2 ) )
= x → 0 lim x 2 ( ( 1 − x 2 + x 2 ) ( 1 + 1 − x 2 ) x 2 )
= x → 0 lim ( 1 − x 2 + x 2 ) ( 1 + 1 − x 2 ) 1
= ( 1 − 0 2 + 0 2 ) ( 1 + 1 − 0 2 ) 1 = 0 . 5