A calculus problem by Akshay Yadav
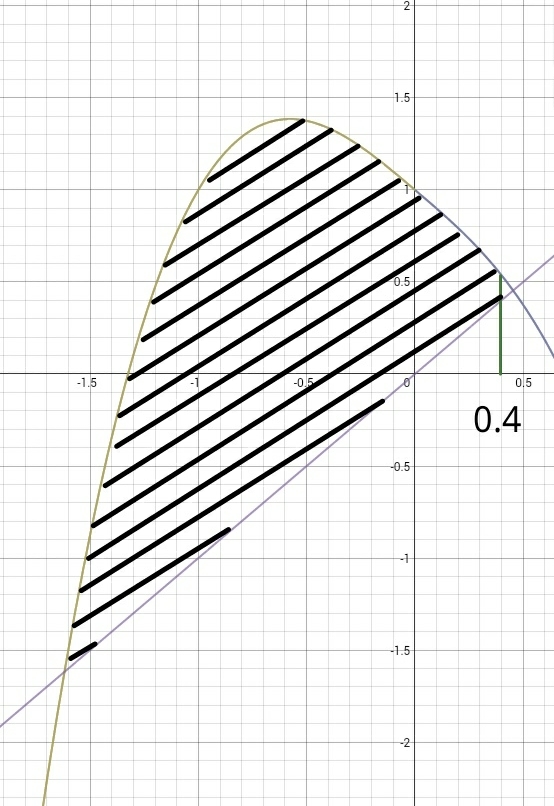
Find the area of given shaded part if the equation of curve is and the equation of line is .
If it can be written as . Where and are pair of mutually prime positive integers and is square root free.
Then find .
Clarifications: The area you have to find is bounded by on the right.
The answer is 11806.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It's a delight to do calculations of this question without a calculator :-).....
First let us find the point of intersection of line and curve in third quadrant which is given by: x 3 − x + 1 = x ⟹ x 3 − 2 x + 1 = 0 ⟹ ( x − 1 ) ( x 2 + x − 1 ) = 0 ⟹ x = 2 − 1 − 5 = − ϕ ( ∵ x < 0 ) Area of shaded part is given by:- T = ∫ − ϕ 0 ( x 3 − 2 x + 1 ) d x + ∫ 0 0 . 4 ( − x 3 − 2 x + 1 ) d x = ( 4 x 4 − x 2 + x ) ∣ − ϕ 0 + ( 4 − x 4 − x 2 + x ) ∣ 0 5 2 = ( ϕ 2 − ϕ − 4 ϕ 4 ) + 6 2 5 1 4 6 Putting ϕ = 2 1 + 5 and simplification gives:- T = 5 0 0 0 6 7 9 3 + 8 5 5 ∴ 6 7 9 3 + 5 0 0 0 + 5 + 8 = 1 1 8 0 6
Note:-I have used everywhere the fact that ∣ x 3 ∣ = x 3 when x > 0 and ∣ x 3 ∣ = − x 3 when x < 0 .