A Peculiar Locus Area
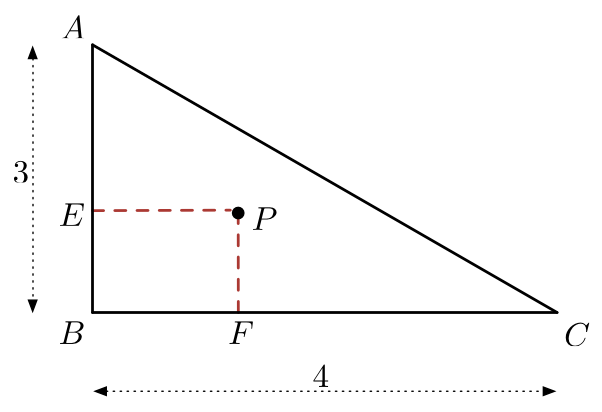 △
A
B
C
is constructed such that
A
B
=
3
,
B
C
=
4
, and
∠
A
B
C
=
9
0
∘
. Point
P
is chosen inside
△
A
B
C
, and points
E
and
F
are drawn such that they form line segments with
P
that are perpendicular to sides
A
B
and
B
C
, respectively. If
L
is the locus of all points
P
such that
[
P
E
B
F
]
≥
1
, then find the value of
⌊
1
0
0
0
[
A
B
C
]
[
L
]
⌋
△
A
B
C
is constructed such that
A
B
=
3
,
B
C
=
4
, and
∠
A
B
C
=
9
0
∘
. Point
P
is chosen inside
△
A
B
C
, and points
E
and
F
are drawn such that they form line segments with
P
that are perpendicular to sides
A
B
and
B
C
, respectively. If
L
is the locus of all points
P
such that
[
P
E
B
F
]
≥
1
, then find the value of
⌊
1
0
0
0
[
A
B
C
]
[
L
]
⌋
Details and Assumptions:
[ N ] means the area of the locus N , and [ P Q R S ] means the area of P Q R S . ⌊ x ⌋ is the floor function.
The answer is 434.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Good problem, Daniel.
Did it in exactly the same way.
That was way deeper than i expected it to be. Good job, man. I'm just a caveman algebra II mathematician
This really took me a lot of attempts to figure out. Here is my solution( Sorry for the bad image quality and clarity):
 image
image
One can easily find the co-ordinates P , Q , R , S by solving x y = 1 and 4 x + 3 y = 1 .
So now [ L ] = [ P Q R S ] − shaded area = 2 6 − l n ( 5 + 2 6 ) .
Thus we have ⌊ 1 0 0 0 [ A B C ] [ L ] ⌋ = 4 3 4 .
good work .....!!
if we put point B on the center of our cartesian coordinate, the equation of the hypotenuse is 3 x + 4 y = 1 2
the key is the we want the find the area of loci x y > = 1 ↔ y > = x 1 bounded by 3 x + 4 y = 1 2 and their point of intersection.
thus, we want to find the integral: ∫ 2 − 2 / 3 ( 6 ) 2 + 2 / 3 ( 6 ) 4 1 2 − 3 x − x 1 d x
the rest is just some tedious algebra
Let A = ( 0 , 3 ) , B = ( 0 , 0 ) , and C = ( 4 , 0 ) . We can see that A C can be expressed as the equation y = − 4 3 x + 3 .
Note that the border of L must satisfy that any point P on it has [ P E B F ] = 1 . Suppose that P = ( x , y ) . We must have y = x 1 in order to have [ P E B F ] = 1 . Therefore, the equation of the border of the locus L is y = x 1 .
We have now reduced the problem to finding the area in between the two equations y = − 4 3 x + 3 and y = x 1 . This calls for a definite integral! We must first find the upper and lower bound. This is when the two functions cross.
We set − 4 3 x + 3 = x 1 . Simplifying, we have that 3 x 2 − 1 2 x + 4 = 0 and using the quadratic equation, we obtain that x = 2 ± 3 2 6 .
Thus, we want to find the value of ∫ 2 − 3 2 6 2 + 3 2 6 ( − 4 3 x + 3 ) − ( x 1 ) d x
Taking the indefinite integral first, we see that ∫ ( − 4 3 x + 3 ) − ( x 1 ) d x = − 8 3 x 2 + 3 x − ln ∣ x ∣ + C . Now, we need to evaluate − 8 3 x 2 + 3 x − ln ∣ x ∣ ∣ ∣ ∣ ∣ 2 − 3 2 6 2 + 3 2 6
Plugging and chugging, the above turns out to be 2 6 + ln ( 5 − 2 6 ) ≈ 2 . 6 0 6 5 4 7 8 1 6 .
Our desired answer is therefore ⌊ 1 0 0 0 6 2 . 6 0 6 5 4 7 8 1 6 ⌋ = 4 3 4 .