A calculus problem by A Former Brilliant Member
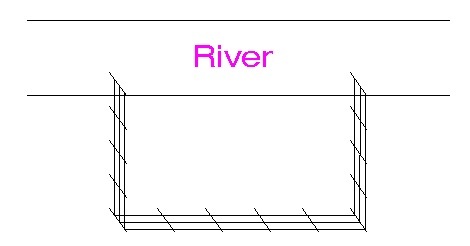 A rectangular field is to be fenced off along the bank of a river where no fence is required along the bank. If the material for the fence costs
per running foot for the two ends and
per running foot for the side parallel to the river, find the largest possible area in
that can be enclosed with
worth of fence.
A rectangular field is to be fenced off along the bank of a river where no fence is required along the bank. If the material for the fence costs
per running foot for the two ends and
per running foot for the side parallel to the river, find the largest possible area in
that can be enclosed with
worth of fence.
The answer is 16875.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The area of the fence is A = x y = x ( 3 0 0 − 3 4 x ) = 3 0 0 x − 3 4 x 2
Differentiate both sides with respect to x ,
A = 3 0 0 x − 3 4 x 2 ⟹ d x d A = 3 0 0 − 3 4 ( 2 x ) = 3 0 0 − 3 8 x
set d x d A = 0
3 0 0 − 3 8 x = 0
3 8 x = 3 0 0
x = 8 3 ( 3 0 0 ) = 1 1 2 . 5
Solving for y , we get
y = 3 0 0 − 3 4 ( 1 1 2 . 5 ) = 1 5 0
The largest possible area is
A = x y = 1 1 2 . 5 ( 1 5 0 ) = 1 6 8 7 5 f t 2