A calculus problem by A Former Brilliant Member
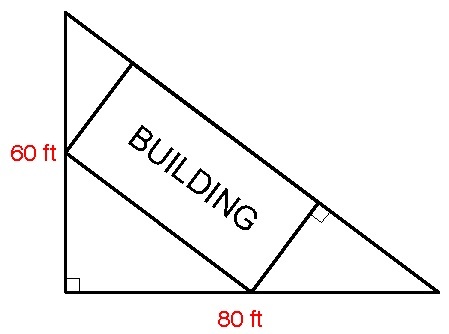 The figure above shows a lot in the form of a right triangle. The largest rectangular building is to be erected so that the longest side lies on the hypotenuse as shown. Find the length of the longest side of the building in feet.
The figure above shows a lot in the form of a right triangle. The largest rectangular building is to be erected so that the longest side lies on the hypotenuse as shown. Find the length of the longest side of the building in feet.
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By similar triangles, we have, a y = 8 0 6 0 ⟹ a = 3 4 y
By similar triangles again, 1 0 0 − x − a y = 6 0 8 0 ⟹ y = 3 4 ( 1 0 0 − x − a )
However, a = 3 4 y , so
y = 3 4 ( 1 0 0 − x − 3 4 y ) ⟹ 4 3 y = 1 0 0 − x − 3 4 y ⟹ 1 2 2 5 y = 1 0 0 − x ⟹ y = 2 5 1 2 ( 1 0 0 − x )
A = x y = x ( 2 5 1 2 ( 1 0 0 − x ) ) = 2 5 1 2 ( 1 0 0 x − x 2 )
Differentiate both sides with respect to x .
d x d A = 2 5 1 2 ( 1 0 0 − 2 x )
Let d x d A = 0
2 5 1 2 ( 1 0 0 − 2 x ) = 0 ⟹ 1 0 0 = 2 x ⟹ x = 5 0 f e e t