An interesting sequence

Calculus Level 3

$\large x^n + x^{n+1} = 1$

For natural number $n$ , let $x_n$ denote the root of the equation above. Evaluate $\displaystyle \lim_{n\to\infty} x_n$ .

The answer is 1.

2 solutions

Akshay Mujumdar
Jun 24, 2015

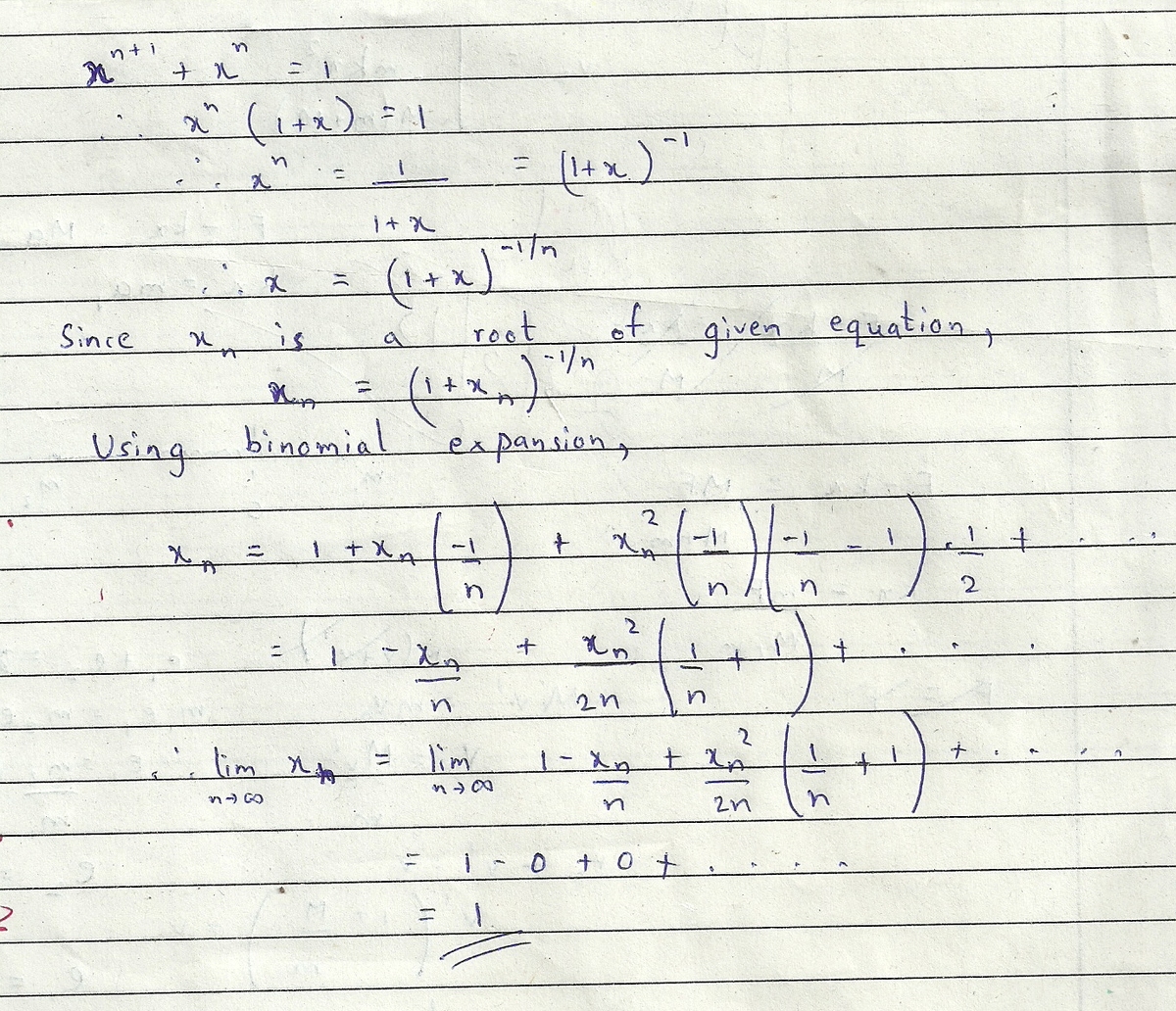You can rearrange this equation and write it as x = (1/(1+x))^(-1/n). Now applying binomial expansion, you can say that x = 1 - (x/n) + ............... Now if n tends to infinity, then the value of the limit comes out to be 1.

Soutrik Bandyopadhyay
Jun 8, 2015

We can modify the LHS by GP formula = $x^{n} * (x^{2} -1)/(x-1)$

The equation thus becomes $x^{n+2}- x^{n}-x+1 = 0$ where x is not 1

As the n blows up to infinity, the root of the equation tends to 1

=> limit is $\boxed{1}$

Moderator note:

Why is this line true?

As the n blows up to infinity, the root of the equation tends to 1

I have a graphical argument to justify this

Consider the graph of $\frac{1}{1+x}- x^{n}$

As n blows up to infinity, the f'(x) at x=1 tends to infinity and x axis cut tends to 1. Thus the root tends to 1

Soutrik Bandyopadhyay - 6 years ago

An interesting sequence

The answer is 1.

2 solutions

Moderator note:

0 pending reports