Nearly a Trigonometric Limit
What is the value of
x → 0 lim sin x − x tan x − x ?
The answer is -2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
ah, the cancellation part is nice :)
Excellent. Did the same. BTW, you could add a bit more detail as to how you applied the L'Hopital's rule so that solution is more complete.
Realising both numerator and denominator has limit approaching 0, L'Hopital rule is something you would wish to try. Applying it you should get cos x − 1 sec 2 x − 1 This might seem complicated to some, but think about secant and cosine: sec x = cos x 1 Substituting this, you should get ( cos 2 x ) ( cos x − 1 ) 1 − cos 2 x Factorising the numerator, we can simplify the whole expression into ( cos 2 x ) ( cos x − 1 ) ( 1 + cos x ) ( 1 − cos x ) = − cos 2 x 1 + cos x which taking the limit gives you -2.
To solve, you must use L'Hopital's rule twice, leaving you with: lim(x-->0) of (2sec^2(x)(tan(x)/(-sin(x)). This equation simplifies down to lim(x-->0) of (2/(-cos^3(x)). Then substitute x=0 into this, and you get 2/(-1)^3, which equals -2
Awesome. L'Hopital is a life saver.
I would just like to point out that the -ve sign shouldn't be inside the brackets.
Not 'must' twice BTW. See other solutions.
I don't know why this is level 2.
lim x → 0 sin x − x tan x − x = = = lim x → 0 cos x − 1 sec 2 x − 1 lim x → 0 − sin x 2 sec 2 x tan x lim x → 0 − cos x 4 sec 2 x tan 2 x + 2 sec 4 x = − 2
w.k.t tanx=x+x^3/3+2x^5/15+17x^7/315+...... so tanx-x= x^3/3+2x^5/15+17x^7/315+...... =x^3 (1/3+2x^2/15+17x^4/315+......) ====> (1) similarly sinx= x-x^3/3+x^5/5-x^7/7+.... so sinx-x= -x^3/3!+x^5/5!-x^7/7!+.... = x^3 (-1/3!+1/5!-1/7!+....) =====>(2) so (1)/(2) we get (1/3+2x^2/15+17x^4/315+......) / (-1/3!+1/5!-1/7!+....) wen we apply limit to it all terms wid x becomes zero... and we will remain with = (1/3) / (1/3!) so answer is '2'
Can we have a non lhopital neither taylor series solution?
We have 2 use L-Hospital's rule. A simple point 2 keep in mind is to: Keep on differenciating both the numerator and denominator until the time your denominater part is a non-zero after you apply the limits. In this problem, we have 2 apply L-Hospital's rule 3 times 2 get the desired result.
Happy solving:)
We can use it just one time and we divide by x^2.
It's basically a problem comes under category of 0/0 form.. So by L'Hospital rule we have to differentiate numerator and denominator separately till we get a proper value after substitution "0" in X...
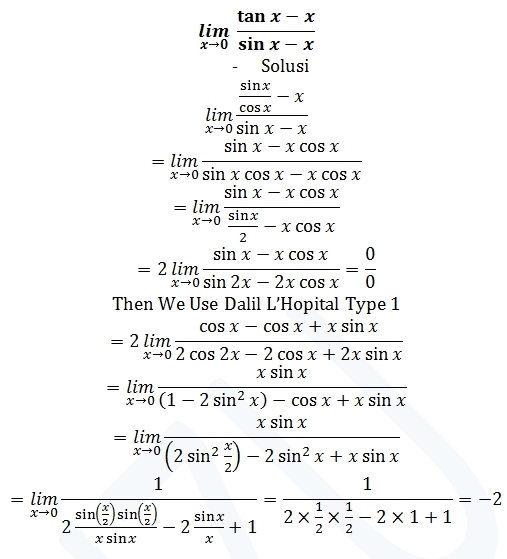
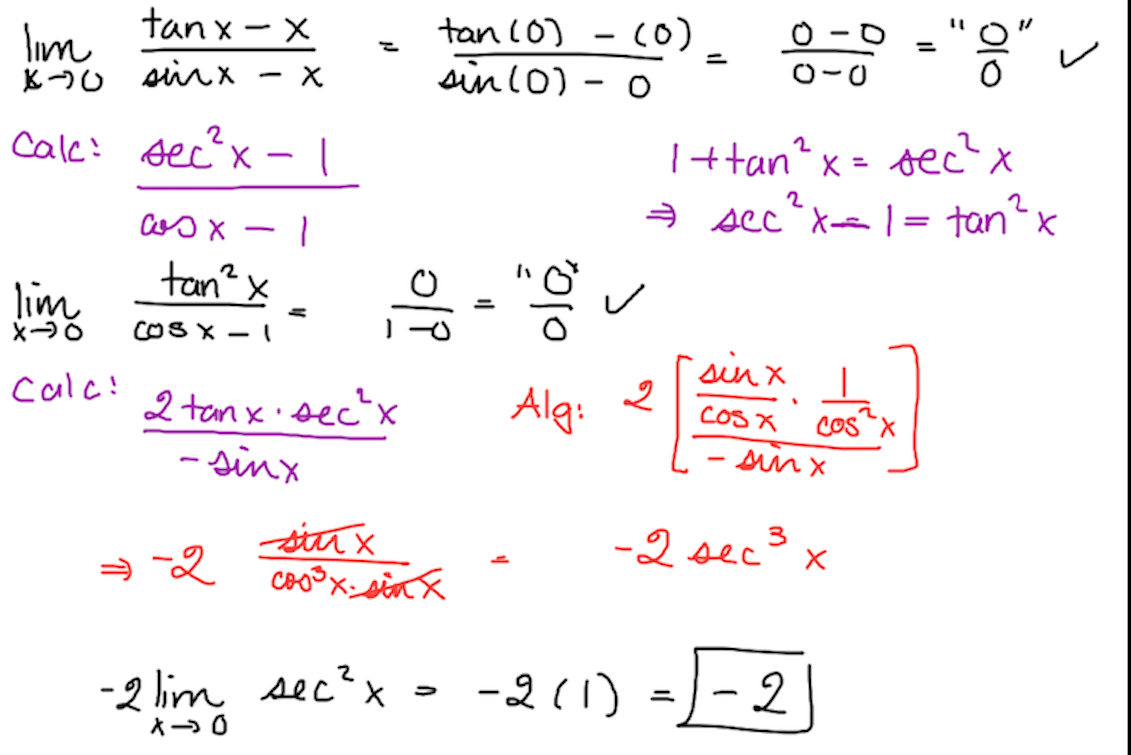
Applying L'Hopital's rule, we can differentiate once and then cancel a factor of cos(x)-1 out of the numerator and denominator. Substituting 0 into the remaining expression, we have -(1+1)/1= -2.