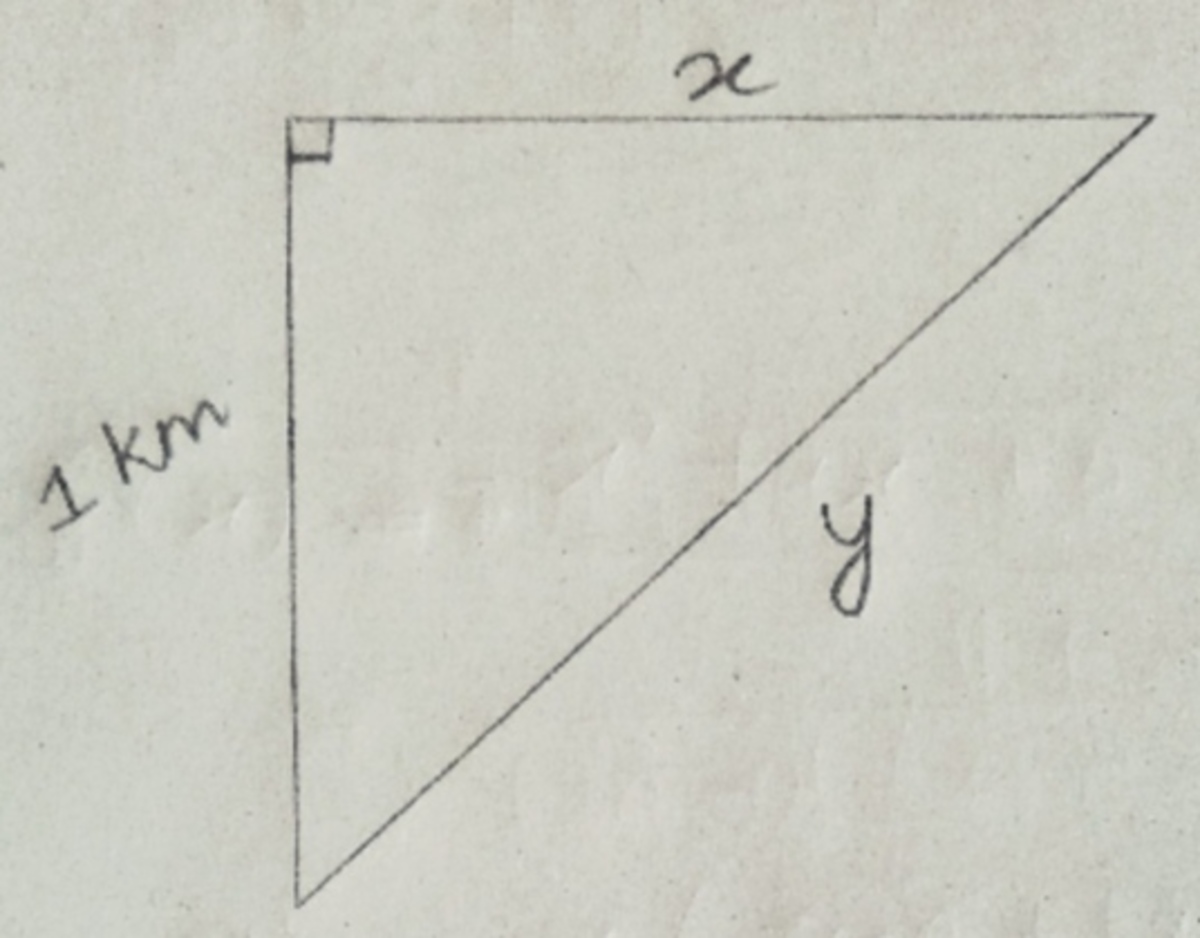
A calculus problem by Pallav Doshi
An aeroplane at an altitude of 1 km is flying horizontally at 800 km/hr passes directly over an observer. Find the rate at which it is approaching the observer when it is 1250 meters away from him.(answer in km/hr)
The answer is 480.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
y 2 ⟹ ( 1 0 0 0 1 2 5 0 ) 2 ⟹ x = x 2 + 1 = x 2 + 1 = 4 3
Differentiating y 2 = x 2 + 1 wrt to time t
2 y d t d y ⟹ d t d y ⟹ v y ⟹ v y = 4 8 0 = 2 x d t d x + 0 = y x ⋅ d t d x = 4 5 4 3 ⋅ 8 0 0