Maximizing Volume Given Closed Area

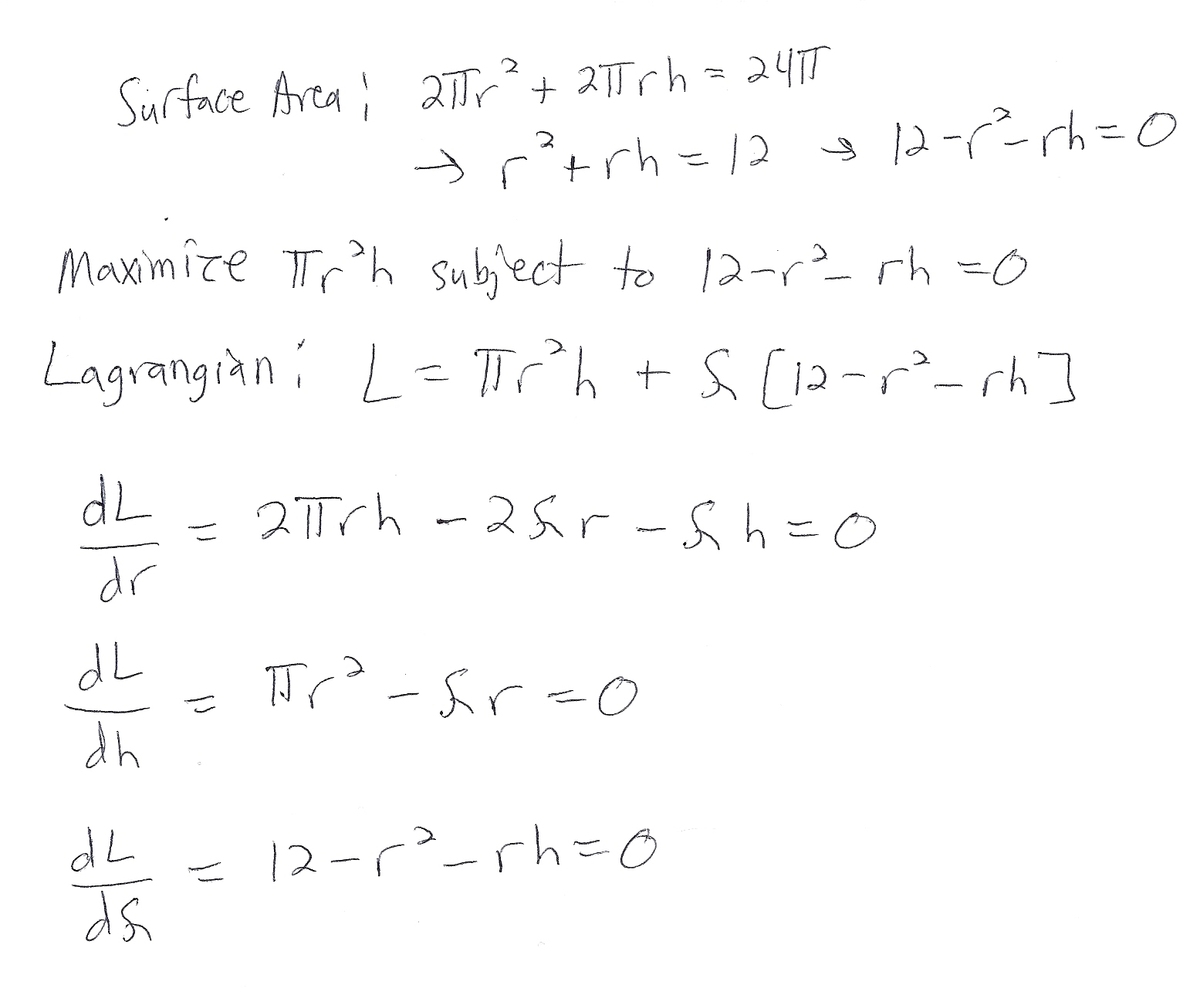
Oh this is nice! I just learned this in my additional math class in high school!

---

Let $S$ and $W$ denote surface area and the volume of this closed cylinder, respectively.

Recall the relevant formula, the surface area and the volume of a cylinder can be expressed as $S = 2 \pi r (r + h)$ and $W = \pi r^2 h$ , respectively, where $r$ and $h$ denotes the radius and height of this cylinder.

We are given that $S = 24\pi$ , so $2\pi r (r+h) = 24\pi \quad \Leftrightarrow \quad r (r+h) = 12 \quad \Leftrightarrow \quad h = \dfrac{12}r - r \; .$

Substitute this expression into the formula of $W$ gives

$W = \pi r^2 h = \pi r^2 \left( \dfrac{12}r - r \right) = \pi (12r - r^3)\; .$

When at the crtical point, $W '= 0$ , with $W' = \pi (12 - 3r^2 ) = 0$ , so $r^2 = \dfrac{12}3 = 4 \Rightarrow r = 2$ only (we take the positive root only because $r$ represents a measurement of distance).

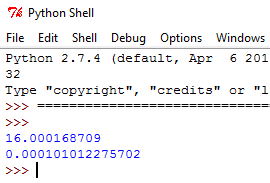
If we substitute the value $r = 2$ into $W$ , we get $W = 16\pi$ .

Now, what's left is to prove that $W$ has a maximum value when $r=2$ . This can be shown by applying the second derivative test , $W'' = \pi(-6r) < 0$ when $r = 2$ .

Since we have shown that $W$ is maximized at $r =2$ and is equal to $16\pi$ , then $V\pi = 16\pi \Rightarrow V= \boxed{16}$ . And we're done!

---

I'm wondering if this question can be solved by applying the arithmetic mean geometric mean inequality or Lagrange multipliers . Thoughts?

Since Christopher asked, here's a Lagrange Multipliers solution. This is not at all the easiest way to solve this problem though. The Lagrangian derivation and resulting equations are shown below. The tricky part is that you have three non-linear equations to solve. Multivariate Newton Raphson or Hill-Climbing algorithms are generally good for such things. In this case, I used a Hill-Climbing algorithm. Essentially, search the (r,h,lambda) parameter space by introducing random mutations to the parameters, and form a "residual" which is equal to the sum of the absolute values of the three nonlinear equations. The residual is ideally zero, and if the particular set of mutated parameters being evaluated yields a smaller residual than the lowest value seen so far, the parameters resulting from the new mutation are kept. Otherwise, discard them and go to the next iteration of the loop. Eventually, the program crushes the residual down to zero and yields the optimal parameters. Python code is attached. One does indeed get a maximum volume of 16 $\pi$ this way.

we could use also an analysis that to maximize the volume the altitude will be equal to its diameter.