This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the answer be x
x = 5 5 5 ⋅ ⋅ ⋅
x = 5 ( 5 5 ⋅ ⋅ ⋅ )
Therefore x = 5 ( x )
x 2 = 5 x
And x = 5
Why this question is so much popular?I have seen this exact question(same no.s) on brilliant about 15 times...!
Thats because it can have so many different variations, ranging from level 1 to level 5. Its so interesting.
I've only seen this problem once.
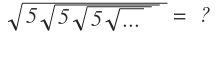
The equation can be written as:
5 x = x
Solving for it gives
x = 5 or 0
Since x > 5 , x = 5