A Challenging Problem of Decahedron With 10 Congruent Right Kite Faces
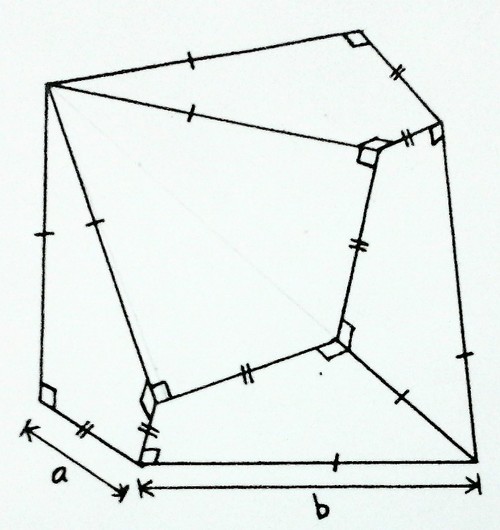 The diagram above shows a decahedron that has 10 congruent faces each as a right kite (i.e. a cyclic quadrilateral consisting of two congruent right triangles with common hypotenuse).
The diagram above shows a decahedron that has 10 congruent faces each as a right kite (i.e. a cyclic quadrilateral consisting of two congruent right triangles with common hypotenuse).
It has two pairs of unequal sides with .
And also has 12 vertices which exactly lie on a spherical surface with certain radius .
If , then what is the value of radius ?
The answer is 11.21511586.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It can be shown (see below) that the smallest angle in the kite is 51.827 and the kite plane is inclined at 48.03 degrees with the equatorial plane of the solid.
Thus the required radius, that is the distance of the pole (where five kites meet) and the center will be ( 1 5 cos 2 5 1 . 8 2 7 + 2 1 5 tan 2 5 1 . 8 2 7 sin 2 5 1 . 8 2 7 ) sin 4 8 = 1 1 . 2
Following is a solution to the rest of the geometry used above
There could be better methods to do this, but here we will use simple high school trig.
Each Kite is a cyclic. So a circle passes through its vertices.
When we look along the axis of the solid, we will see two 'concentric' pentagons with a 36 degree relative rotation. Let the circumradius of these pentagons be 1. Hence side = 2 sin 3 6 Then the above circumcircle of the kite will be seen as an ellipse passing through the common center (axis), one vertex of one pentagon and two straddeling vertices of the other as shown. Clearly the minor axis of this ellipse is 1 and b = 1/2. If we take its equation to be a 2 x 2 + 4 y 2 = 1 we know two points on the ellipse (straddeling vertices of the pentagon) with x = sin 3 6 and y = cos 3 6 − 1 / 2 we can solve for a which is also the circumradius of the kite. a = 0.747674
The angle subtended by half the pentagon side is same as the angle we seek = arcsin ( 0 . 7 4 7 6 7 4 sin 3 6 ) = 5 1 . 8 2 7
Further, the inclination of the kite plane with the equatorial plane can be found to be arccos 0 . 7 4 7 6 7 4 0 . 5 = 4 8 . 0 3