A Challenging Problem of Tetrahedron by H.C.R
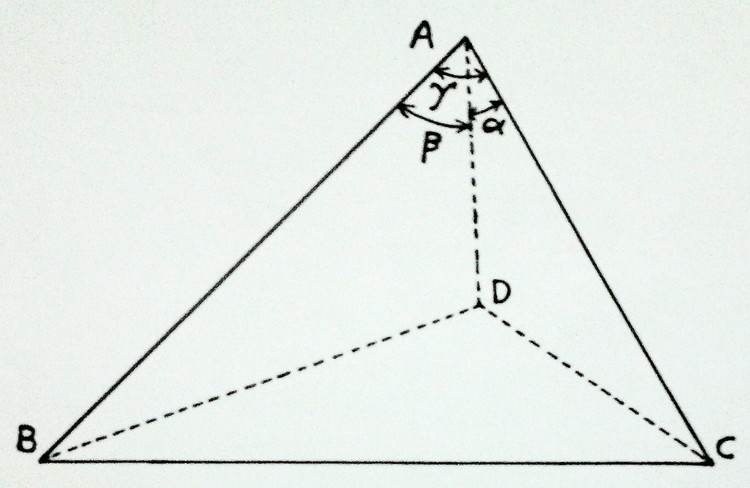 The diagram above shows a tetrahedron with vertices
. If the angles between the lateral edges
&
,
&
and
&
meeting at the vertex
are
respectively, then calculate the correct value (up to three decimal points) of the solid angle (in Ste-radian) subtended by triangular face
at the vertex
.
The diagram above shows a tetrahedron with vertices
. If the angles between the lateral edges
&
,
&
and
&
meeting at the vertex
are
respectively, then calculate the correct value (up to three decimal points) of the solid angle (in Ste-radian) subtended by triangular face
at the vertex
.
The answer is 0.515050552.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
L e t θ = 2 1 ∗ ( α + β + γ ) = 2 0 + 3 5 + 4 2 . 5 = 9 7 . 5 . ∴ 2 θ = 4 8 . 7 5 , 2 θ − α = 2 8 . 7 5 , 2 θ − β = 1 3 . 7 5 , 2 θ − γ = 6 . 2 5 . I f Ω is the solid angle, we have, T a n 4 Ω = ( T a n 2 θ ) ∗ ( T a n 2 θ − α ) ∗ ( T a n 2 θ − β ) ∗ ( T a n 2 θ − γ ) = T a n 4 8 . 7 5 ∗ T a n 2 8 . 7 5 ∗ T a n 1 3 . 7 5 ∗ T a n 6 . 2 5 ∴ Ω = 2 9 . 5 1 0 2 . But these angles are in degrees. I m p l i e s Ω = 2 9 . 5 1 0 2 ∗ 1 8 0 π = 0 . 5 1 5 S t e − r a d i a n