A Challenging Problem of Uniform Polyhedron With Right Kite Faces by H.C.R
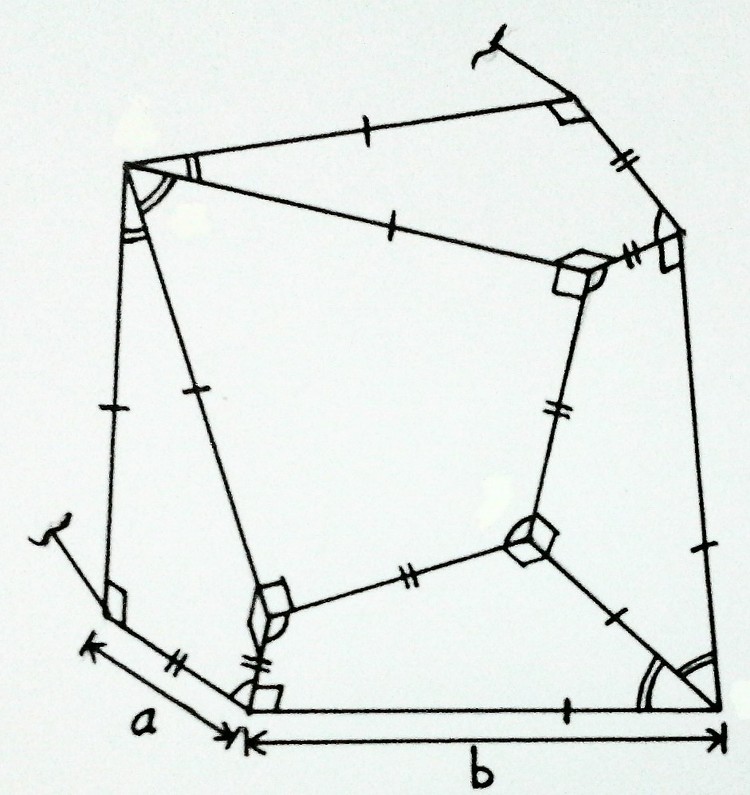 The above picture shows a uniform polyhedron having 1002 vertices lying on a spherical surface, 2000 edges & 1000 congruent faces each as a right kite with two unequal edges of lengths a & b (b>a). Find out the ratio b/a.
The above picture shows a uniform polyhedron having 1002 vertices lying on a spherical surface, 2000 edges & 1000 congruent faces each as a right kite with two unequal edges of lengths a & b (b>a). Find out the ratio b/a.
The answer is 225.0772278.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In general, the ratio of unequal edges say a & b ( a < b ) of a uniform polyhedron having 2 n + 2 vertices lying on a spherical surface, 4 n edges & 2 n congruent faces each as a right kite, is given by following formula (see the detailed analysis of uniform trapezohedron by HC Rajpoot )
b a = tan n π tan 2 n π
As per given problem, no. of edges 2 n + 2 = 1 0 0 2 i.e. n = 5 0 0 , setting the value of n in above general formula
a b = tan 5 0 0 π tan 2 ⋅ 5 0 0 π 1 ≈ 2 2 5 . 0 7 7 2 2 7 8