A Charge Oscillating Above A Charged Square Plate.
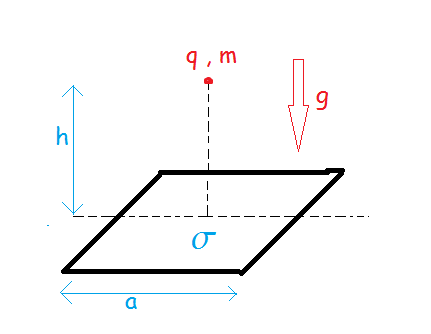 Consider a point charge of mass
m
and charge
q
in equilibrium at a height
h
above a square plate of charge density
σ
and side
a
=
2
h
in the presence of gravity in equilibrium. The plate is fixed.
Consider a point charge of mass
m
and charge
q
in equilibrium at a height
h
above a square plate of charge density
σ
and side
a
=
2
h
in the presence of gravity in equilibrium. The plate is fixed.
Now, the point charge is given a small displacement in vertical displacement. Find an expression for the time period of its oscillations T in terms of h and g , and give the value of 5 3 . 7 2 T for h = 9 m and g = 9 . 8 m / s 2 to the nearest integer
The answer is 308.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Discussions for this problem are now closed
What a awesome solution.
Thanks :)
I got mistaken by a factor of 2 miscalculation. And couldn't figure out what was wrong
Just wanted to ask you Jatin if you modified your question. The time period turns out to be 5.73 seconds and I think that earlier you had asked to compute the value of [ 1 0 0 T ] . However I was marked wrong. Anyway, nice solution :)
I am sorry for any inconvenience. Actually, I had modified it. Sorry again for the time loss .Actually, there was an error in my input to calculator. By the way, how could you have done the problem you posted without calculus?
No problem Jatin! As for my question, I came up with it while this very question. The idea is to use Gauss Law.
I am sure you must be knowing that the flux through the square plate is 6 ϵ 0 q due to the charge (It is quite a popular question).
Now F l u x = ∫ E ⋅ d s
Here E is the field due to the charge.
So F l u x = ∫ E d s cos θ
Multiply both sides by σ and note that σ d s = d q p l a t e :
σ × F l u x = ∫ E d q p l a t e cos θ
Now E d q p l a t e cos θ = d F p l a t e (note that sin θ components cancel due to symmetry).
Thus we have the answer.
Consider a square loop of thickness d x at a distance x from center, such that the side of square is 2 x . Due to each of 4 sides, carrying charge σ d x each electric field's magnitude is 2 π ϵ 0 x 2 + h 2 2 x 2 + h 2 σ x d x
Since the net field is vertical, we take only vertical component , multiplying above expression by x 2 + h 2 h and then multiply by 4 , as there are 4 sides.
Hence, the electric field due to square loop is :
d E = π ϵ 0 ( x 2 + h 2 ) 2 x 2 + h 2 2 σ h x d x
E = π ϵ 0 2 σ h ∫ 0 2 a ( x 2 + h 2 ) 2 x 2 + h 2 x d x
Let 2 x 2 + h 2 = t 2 , and obtain:
E = π ϵ 0 2 σ h ∫ h 2 a 2 + h 2 h 2 + t 2 d t
= π ϵ 0 2 σ ( tan − 1 ( h 2 a 2 + h 2 ) − 4 π )
Note that you get E = 2 ϵ 0 σ for a → ∞ , and also for h → 0 . This verifies the result.
Now, in our case, when a = 2 h , E = 6 ϵ 0 σ as in another problem posted by kartik kannan.
Now, 6 ϵ 0 q σ = m g
Let us change h by a small distance δ x < < 1 . Then by taking derivative of the force,
F n e t = q E − m g
⇒ δ x δ F = q δ x δ E ≈ − 3 π ϵ 0 h q σ
⇒ F n e w = δ F = − π h 2 3 m g δ x
Hence, T = 2 π 2 3 g π h
Put values to get the answer as 3 0 8