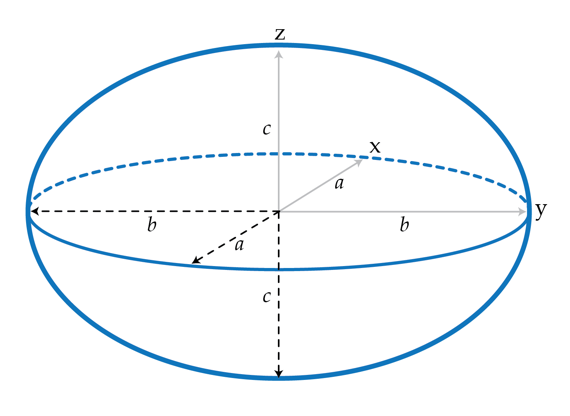
A charged ellipsoid

Gauss' Law shows us that, for a conductor, the Electric field strength, E, at any point is equal to $\sigma/\epsilon_0$ .

E is normal to the surface just outside the conductor, and E inside a conductor is 0. So, if you were to draw a small Gaussian cylinder through surface and use Gauss' law, you would obtain:

$\int_A (\vec{E} \cdot d\vec{A}) = EA + 0(A) = \sigma A/\epsilon_0$ .

Therefore we have $E = \sigma/\epsilon_0$ for any point.

The Electric field strength is strongest at "sharp" points ie. points of highest curvature since there is a greater surface charge density at these points. In an ellipse, the two points of greatest curvature are obviously those on the major axis. (E is equal at both points, of course, due to symmetry reasons)

Therefore, we have:

x = 0 z = 0 y = +- b (the Y- axis is the major axis)

Thus

$\sigma = Q/(4\pi ac)$

and so

$E = Q/(4\ pi\epsilon_0 ac)$ = 15,000 V/m

We know that the electric field is stronger near sharp edges. In fact, the electric field near the surface of a conductor is inversely proportional to the radius of curvature of the surface. It is easy to see that the "sharpest" point of the ellipsoid corresponds to $x=0, y=b, c=0.$ From Gauss's Law we know that the electric field is given by $E(x,y,z)=\frac{\sigma(x,y,z)}{\epsilon_{0}} \rightarrow E_{max}= E(0,b,0)=\frac{Q}{4\pi \epsilon_{0} ac}=15 \textrm{kV/m}.$ Analogously, we find that the minimum electric field corresponds to $x=a, y=0, z=0$ and $E_{min}=6 \textrm{kV/m}.$ Note that electric field is maximal when $\frac{x^{2}}{a^{4}} +\frac{y^{2}}{b^{4}}+ \frac{z^{2}}{c^{4}}$ subject to the constraint ${\frac{x^{2}}{a^{2}} +\frac{y^{2}}{b^{2}}+ \frac{z^{2}}{c^{2}}}=1.$ This is equivalent to the minimization of $(\frac{1}{a^{2}}-\frac{1}{b^{2}})\frac{x^{2}}{a^{2}}+ (\frac{1}{c^{2}}-\frac{1}{b^{2}})\frac{z^{2}}{c^{2}}+\frac{1}{b^{2}}$ Since $a<b$ and $c<b$ , the minimum corresponds to the point $x=0, z=0$ .

The quick and dirty method is to use the fact that the electric field near the surface of a conductor is usually strongest near sharp curves or edges. Thus we would expect the maximum electric field to occur at the point x = 0, y = b, and z = 0. Let's see if this is indeed the case.

The magnitude of the electric field E near the surface of a conductor is given by $E={\frac {\sigma}{\epsilon_{{0}}}}$ . Substituting in our equation for $\sigma$ and using the identity $K={\frac {1}{4\pi \,\epsilon_{{0}}}}$ results in $E = {\frac {QK}{abc}}{\frac {1}{\sqrt {{\frac {{x}^{2}}{{a}^{4}}}+{\frac {{y}^{2}}{{b}^{4}}}+{\frac {{z}^{2}}{{c}^{4}}}}}}$ . We want to maximize this function on the surface of the ellipsoid. This is the same as minimizing the function ${\frac {{x}^{2}}{{a}^{4}}}+{\frac {{y}^{2}}{{b}^{4}}}+{\frac {{z}^{2}}{{c}^{4}}}$ under the same constraint. This minimization can be efficiently carried out using Lagrange multipliers. We get the following equations for some constant k: \(\begin{array}{clcr} {\frac {2x}{{a}^{4}}}= k \* {\frac {2x}{{a}^{2}}} \\

\{\\frac \{2y\}\{\{b\}^\{4\}\}\}= k \\\* \{\\frac \{2y\}\{\{b\}^\{2\}\}\}    \\\\

\{\\frac \{2z\}\{\{c\}^\{4\}\}\}= k \\\* \{\\frac \{2z\}\{\{c\}^\{2\}\}\}

\end{array}\)

It is not hard to see that this system is inconsistent unless two of x, y, and z are 0. This is because a\neq b \neq c (try solving for k when 2 or 3 of x,y, and z are nonzero). So we have three possibilities for (x,y,z): (0, 0, c), (0, b, 0), and (a, 0, 0) (the point (0, 0,0) is excluded because it does not lie on the surface of the ellipsoid). Whichever of these three points gives the largest E will be our maximum. We find: \(\begin{array}{clcr} E(0, 0, c) = 9000 V/m \\

E\(0, b, 0\) = 15000 V/m  \\\\

E\(a, 0, 0\) = 6000 V/m

\end{array}\)

So our maximum is E(0, b, 0) = 15000 V/m. Note that this matches our intuitive guess.

The potential increases on the tips, then the potential will be maximum at the point where the surface is most curve, it can be clearly seen that the most curve region is when y=b, x=z=0, substituting these values we have the potential V=1500v

1.find max charge density that come on 0,5,0 [by analyzing ellipsoid eq.and given charge den. expression} 2.electric field =charge density/permittivity