Shifts and Signals

Chemistry Level 3

An extension to Teleanu Florin's problem (for context you might want to go through his problem)

This is the compound that was investigated in the problem, we call it compound X :

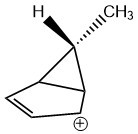
Let all the hydrogen atoms bonded to the carbon atoms in the cyclopentane ring be denoted as Ring Hydrogens or $H_{r}$ and the remaining hydrogen on the top of the cyclopropane ring be called the Axial Hydrogen or $H_{a}$ . The hydrogen atoms present in the axial methyl group are denoted as $H_{m}$ .

Let's say we have some kind of reaction that allows us to remove a $H_{r}$ atom and replace it with a deuterium ( $D_{r}$ ) without changing the rest of the molecule.

We now turn to H-NMR spectra of 3 compounds:

Compound X
Compound Y (one $H_{r}$ is replaced)
Compound Z (two $H_{r}$ are replaced)

(All compounds are placed in solutions that are above 390K)

We now define 2 quantities $\alpha$ and $\beta$ . $\alpha$ is the number of H-NMR signals obtained from compound Y and $\beta$ is the number of H-NMR signals obtained from compound Z

What is the value $\alpha$ - $\beta$ ?

Bonus :

Devise a reaction that can replace $H_{r}$ with $D_{r}$

The answer is 0.

1 solution

Vitthal Yellambalse
Oct 14, 2016

As Teleanu Florin points out in his solution, the HOMO (Highest Occupied Molecular Orbital) of the $C_{4}$ and $C_{5}$ bond and the LUMO (Lowest Occupied Molecular Orbital) of $C_{1}$ ie., the empty p-orbital are involved in a [1 4] electrocyclic shift. This is illustrated below:

However this process repeats infinitely, hence there exist in 5 canonical forms. These 5 forms are shown below:

These canonical forms create a resonance hybrid . This explains why the H-NMR spectra of the compound never changes even though an infinite number of [1 4] shifts occur while observing it. (It looks like a capped pentagon)

Using the yet to be determined reaction mechanism (YDRM) we generate compound Y :

Each signal in a H-NMR represents a different chemical environment that hydrogen can be placed in.It is important to note that deuterium atoms are invisible to the H-NMR spectra.

Hence in compound Y we see 4 unique environments:

Positions adjacent to the deuterium atom that are on the pentagon ( two of such exist )
Positions that are one atom away from the deuterium atom and are still on the pentagon ( two of such exist )
The position occupied by the $H_{a}$ atom
Positions at which $H_{m}$ are present ( three of such exist )

Since four unique environments exist $\implies$ $\alpha = 4$

We use YDRM again to generate compound Z . We now encounter a problem, the new deuterium atom can either be placed adjacent to the first deuterium atom or be placed one atom away from it.

CASE ONE : Deuterium atoms are adjacent to each other

In compound $Z_{1}$ there exist:

Positions adjacent to the two deuterium atoms that are on the pentagon ( two of such exist )
The position that is one atom away from the two deuterium atom and is still on the pentagon
The position occupied by the $H_{a}$ atom
Positions at which $H_{m}$ are present ( three of such exist )

Since four unique environments exist, $\beta_{1} = 4$

CASE TWO : Deuterium atoms are separated by one $H_{r}$

In compound $Z_{2}$ there exist:

The position sandwiched between the two deuterium atoms.
Positions that are on the pentagon but aren't sandwiched between the two deuterium atoms ( two of such exist )
The position occupied by the $H_{a}$ atom
Positions at which $H_{m}$ are present ( three of such exist )

Again four unique environments exist, $\beta_{2} = 4$

Since $\beta_{1} = \beta_{2}$ $\implies$ $\beta = 4$

So the answer is $\boxed{ \alpha - \beta = 0 }$

Side note:

If you can design a reaction mechanism that does what YDRM is designed to do, please let me know. I still haven't been able to design one.

Very nicely explained 👌

Aniket Sanghi - 4 years, 4 months ago

Shifts and Signals

The answer is 0.

1 solution

0 pending reports