A Chord Frenzy
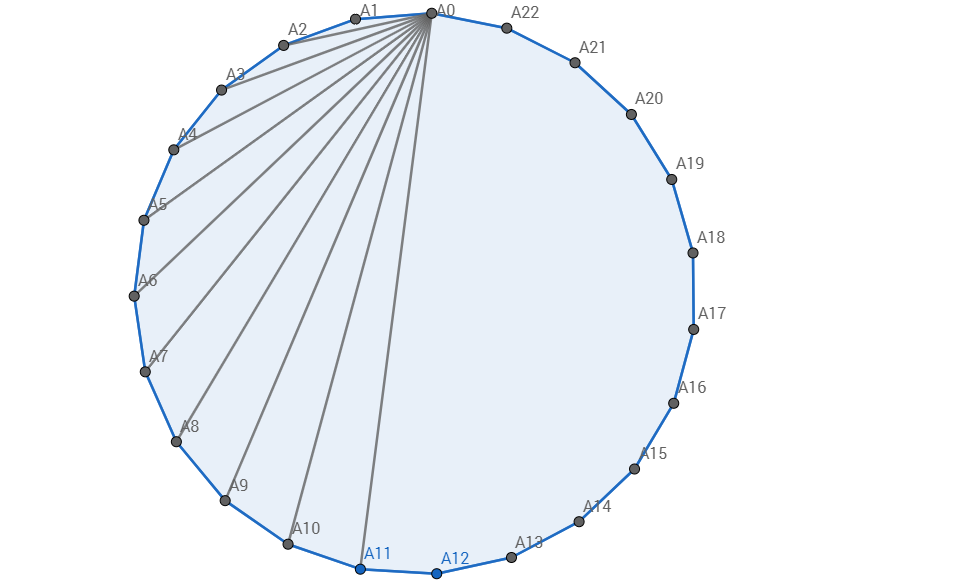
Assume the polygon above is inscribed in a circle of radius r .
A regular n -gon is inscribed in a circle with radius r .
Let A 0 , A 1 , A 2 , . . . , A n − 1 be the vertices of the n -gon inscribed in the circle. Draw chords A 0 A 1 , A 0 A 2 , A 0 A 3 , . . . , A 0 A k , where k < n .
Write an computer algorithm to compute P = ( ∏ j = 1 k A 0 A j ) 2 , then letting r = 2 , n = 2 3 , and k = 1 1 , find P = ( ∏ j = 1 1 1 A 0 A j ) 2 .
The answer is 96468992.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For General Case:
Let u 0 = 2 r sin ( n π ) and for ( 1 ≤ j ≤ k − 1 ) let u j = u 0 2 + u j − 1 2 − 2 a 0 a j − 1 cos ( n ( n − 2 ) π − ( j − 1 ) n π )
and P = ( ∏ j = 0 k − 1 u j ) 2 .
Program(written in Free Pascal):
Using the program and r = 2 , n = 2 3 , and k = 1 1 we obtain P = ( ∏ j = 0 1 0 u j ) 2 = 9 6 4 6 8 9 9 2 .