A circle, a triangle, and a 24-gon

In the figure, we know the following:

• Segment $GM$ is parallel to segment $HI,$ and segments $EB, FC, GD$ are all parallel to one another.
• $EA=2, BA=y, FE=y-1, BC=2x, FG=7, CD=3y+2, \angle FGM=60^\circ.$
• Triangle $AGD$ is inscribed in circle $O.$
• Extending segment $AD$ to point $H$ and further makes it meet one of the vertices of a regular icositetragon (also known as icosikaitetragon or tetracosagon or a 24-gon), 4 of whose vertices are $K, H, I, J.$

What is the area of sector $AOD?$

If your answer can be expressed in the form $\pi\big( b - c\sqrt{d} + e\sqrt{f} - e \sqrt{c} \big),$ where $d, f, c$ are square-free, $c$ and $f$ are prime, and the expression cannot be simplified furthur, determine the value of $b+c+d+e+f.$

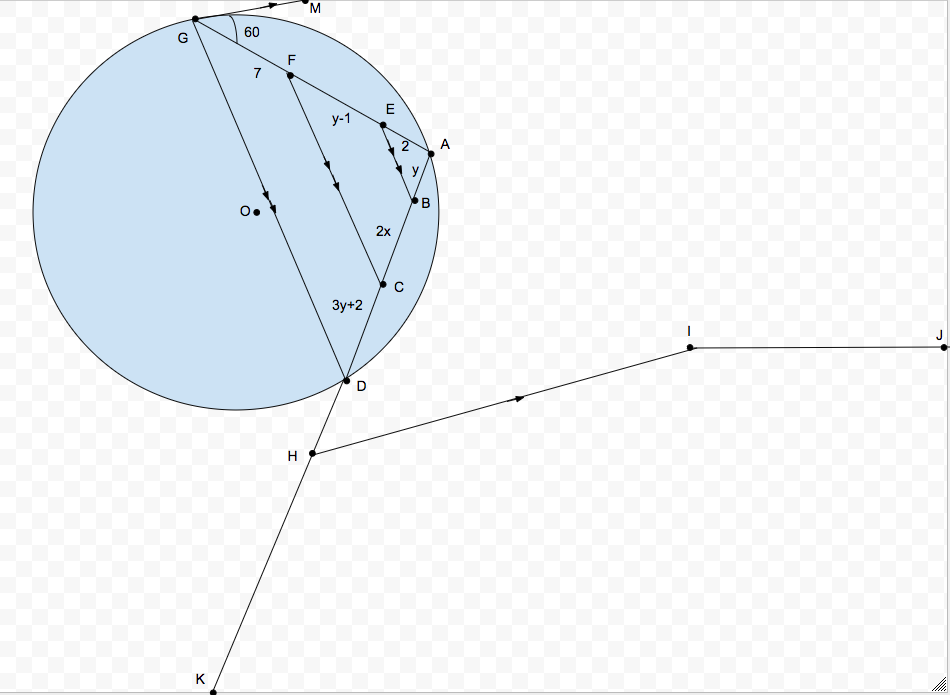
Note: Trigonometry may be used for this problem. No calculators allowed.